- Messages
- 95
- Reaction score
- 35
- Points
- 28
the answer for the functions was g(x) only because the f(x) cannot be equall to the inverse when the values of "X"s are same. so the answer is SOLELY g(X)
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
No he is talking about the qusetions previous to the ones u r talking about.21 AND 42 HOW ?????????
THEY WERE 38 AND 40
Isnt 1D suppose to be $90 as it said round to the nearest cent.
3rd question last part is something like 2177.5(OR 2117.5) as for cost the answer should be to 2 d.p.
9th question(probability) last part the answer is 781/1024
10b the answer is x-1=g^-1(X) 10th question last one was g(x)
Last page the answers were : 1/3 , 1/5, 1/4, 1/6 , 0.363
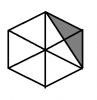
Hello bro.. I think the answer you have mentioned for the last page answers for the 4th diagram is incorrect. The shape given was a hexagon and a triangle was drawn inside it. So you can only draw a maximum of 3 more triangle inside the shape of the hexagon. So the total no of triangles that can be drawn inside the hexagon will only be 4. As only one triangle was shaded, the shaded area would be 1/4 and not 1/6. Hope i am clear in my explanation.
Isnt 1D suppose to be $90 as it said round to the nearest cent.
Oh my bad. Yeah its suppose to be 89.99Actually, nearest cent means nearest $0.01.
So the correct answer would be $89.99, as $90 is to the nearest DOLLAR.
Mate you mixed up the functions, f(x)=1/x and g(x)=1-xActually, the way I remember it:
f(x) = 1 - x
g(x) = 1/x
If you find the inverse of both of these you'll see:
f^-1(x) = 1 - x
g^-1(x) = 1/x
You can even try inputting random numbers in the function, taking the output, then inputting that output into the function to see whether it comes back to the input:
f(12) = 1 - (12) = -11
f(-11) = 1 - (-11) = 12
g(5) = 1/(5) = 0.2
g(0.2) = 1/(0.2) = 5
Therefore, it's both f(x) and g(x)
Mate you mixed up the functions, f(x)=1/x and g(x)=1-x
And the condition for the question was that the VALUE OF X SHOULD BE SAME IN THE INVERSE AND ORIGINAL funtion, so its clearly g(x) not both
Prove: g(0)=g^-1(0)
1-0=1-0
1=1
Well ****! Gonna loose marksOkay so;
f(x) = 1/x
and just prove that:
f(2) = f^-1(2)
To prove the above, we must also know what f^-1(x) is. Just try working out what f^-1(x) comes to. You'll see f^-1(x) = 1/x. So:
f(2) = f^-1(2)
1/2 = 1/2
0.5 = 0.5
You already agree with g(x), it's f(x) as well.
But I don't think they asked for two functions bro! And the question was also only for one mark!Well ****! Gonna loose marks
Well i also had a question that in f(x) if the value is zero it doesnt work so isnt the answer suppose to be g(X)?But I don't think they asked for two functions bro! And the question was also only for one mark!
So are two answers really required?
But I don't think they asked for two functions bro! And the question was also only for one mark!
So are two answers really required?
Well i also had a question that in f(x) if the value is zero it doesnt work so isnt the answer suppose to be g(X)?
Well i also had a question that in f(x) if the value is zero it doesnt work so isnt the answer suppose to be g(X)?
Just relax bro! Hope the examiner accepts one answer..
Moreover, it will be better if you remember the question fully and type it here.
Did the question say "for any value of x"? If it said so, then f(x) would not be the answer.
The question did not say "for any value of x"....
And as I've already said previously, even if x=0 were to be considered, both f(x) and f^-1(x) give the value undefined... which is equal.
Hmm. thanx, u sound like a good mathematician.Actually, it said WHICH of the functions.... so it's not necessarily only one answer.... as for it being only 1 mark, I think it was to make it less obvious that there were two answers...
The question actually defined f(x) to be:
f(x) = 1/x , x ≠ 0
That actually means f(x) is not defined at x=0, so one should not consider the point when x=0.
But even if you were to take x =0, we would prove:
f(0) = f^-1(0)
undefined = undefined.
So that's sort of proven as well
Though really, x=0 should not be considered.
Hmm. thanx, u sound like a good mathematician.
For almost 10 years, the site XtremePapers has been trying very hard to serve its users.
However, we are now struggling to cover its operational costs due to unforeseen circumstances. If we helped you in any way, kindly contribute and be the part of this effort. No act of kindness, no matter how small, is ever wasted.
Click here to Donate Now