Mathematics: Post your doubts here!

[Dsilentkila]

salam folks.
got a question ,
Paper 4 (41) , MJ 2010.
Q8.d.iii .
thanks alot in advance

 

[Saad the Paki]

Can any one help me in part ii
i wrote answer frm 2 to 10 but answer is frm -4 to 2
can someone explain how....... i cannot understand

I think u didmt understand the question properly.. they asked for the MINIMUM values.. other wise the graph can go on forever and the range will be huge.. so from the graph approx 2 and -4 r the minimum values from wich u can get only one solution

 

[Shada Mohammed]

11 part b)i)
The numbers of smallest triangles as power of 2 are increasing powers by 2.
Hence after 2^4, it'll be 2^6, 2^8 etc.
Work out 2^6, and 2^8 and put its values in number of smallest triangles row.

6c)
Probability of choosing a N is 2/6. So probabibility of NOT getting N is (1-2/6) which is 4/6.
Hence till 4th card probability will be:
4/6 * 3/5 * 2/4 * 2/3, which is 2/15. The denominators are decreasing, because cards are being chosen without replacement.

_______________________________________________________________________
Question 11:
Okay, if the total area of the shapes is X. And the area of the shaded part is k. It means k is a number that is multiplied with the area to give shaded area.
For example in the first one, if the total area of a triangle is X, and the shaded area is 1/3 of the total area (of X). Then to calculate this shaded area it'll be 1/3 * X. In this case k is 1/3. It's a number multiplied by X (total area) to give the shaded area.
Now the second one, We can calculate the area of the sector by 72/360 * pi * radius squared. If the total area (X) of the circle is pi * radius squared, what are you multiplying with it to get shaded area? That's 72/360. So 72/360 is k.
For the third one, EF = FG, hence if we assume EF is 1, then FG will also be 1. Therefore EG will be 2. Now since they are similar triangles, (EF/EG)squared will give area. Therefore 1squared/2squared is answer. which is equal to 1/4.
For the fourth one, a hexagon is made of 6 equilateral triangles. Hence each angle will be 60 degrees. So to find total area (X) it'll be 6 * length * length * sin60. now the area that is shaded has the same area as any triangle from the center to the two sides. So they want to find area of only 1 triangle out of the 6 triangles. Hence k will be 1/6.
Last one, shaded area is area of sector - area of triangle. Which is 90/360*pi*radius squared - 1/2 * radius squared. Work this out and factorise, it'll give 1/4*radius squared (pi - 2). Now this is the shaded area. They want k which is the value you multiply with the whole sector to give this shaded area. so divide the shaded area by area of whole sector. the answer will be pi - 2/pi.

Question 9)e):
Now probability that the weather is fine is 3/4. Now if the weather is fine for 5 consecutive days the probability will be (3/4)^5. So probability that it is NOT fine for 5 consecutive days will be 1 - (3/4)^5. Your working was wrong because it depicts that weather was fine for the first four days, then fifth day it was not fine. You didn't take to account that the weather could not be fine on the 1st, 2nd, 3rd or 4th day even. Hence this is the best method.

Cheers

Thanks a lot

 

[NOneed2speedd]

I think u didmt understand the question properly.. they asked for the MINIMUM values.. other wise the graph can go on forever and the range will be huge.. so from the graph approx 2 and -4 r the minimum values from wich u can get only one solution

How can u get one... like for example if i take 1 then y=1 is cutting the curve 3 times

 

[Saad the Paki]

How can u get one... like for example if i take 1 then y=1 is cutting the curve 3 times

No... they mean such a line that will only cut the curve once ... so any line greater or equal to y=2 and less than and equal to y=-4 will only cut the graph once... U can check it out

 

[masterex567]

so will u be giving variant 22 and 42?

Yeah! Also you?

 

[NOneed2speedd]

No... they mean such a line that will only cut the curve once ... so any line greater or equal to y=2 and less than and equal to y=-4 will only cut the graph once... U can check it out

Oh ok.... thanks again for helping

 

[Saad the Paki]

Yeah! Also you?

Yup.! So u have these papers on.....?

 

[Saad the Paki]

Find the nth tern for this sequence
2,3,5,8,13,21....

 

[Lana19984]

http://www.thamerinternationalschool.com/uploads/files/0580_w09_qp_21.pdf
Would anyone please help me with question 21 part b ? i dont understand how the answer is 960 m
PLEASE HELP

 

[Lana19984]

Find the nth tern for this sequence
2,3,5,8,13,21....

This is actually Fibonacci sequence where each number is equal to the two terms before it so the general formula is X(n-1)+X(n-2)=n (which means the two values before it )
this however isnt the nth term the nth term would include the golden ratio such that

,
however this wont work on the sequence you have and changes are needed to be done since the first term isnt 1 , would you tell me which past paper or book did this come from ?

 

[Saad the Paki]

This is actually Fibonacci sequence where each number is equal to the two terms before it so the general formula is X(n-1)+X(n-2)=n (which means the two values before it )
this however isnt the nth term the nth term would include the golden ratio such that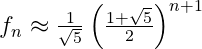

,
however this wont work on the sequence you have and changes are needed to be done since the first term isnt 1 , would you tell me which past paper or book did this come from ?

This is from 0580 O/N 2006 P2 Q9
They dont actually ask to find the nth term but they ask fot the next term so i was confused

 

[Lana19984]

This is from 0580 O/N 2006 P2 Q9
They dont actually ask to find the nth term but they ask fot the next term so i was confused

alright good cause finding the nth term for this would take alot of time i suppose and i dont think its in the syllabus

 

[misscute406]

Can someone help me out in this question please?? 0580/22/m/j/14 Question 18

The two containers are mathematically similar in shape.
The larger container has a volume of 3456cm3 and a surface area of 1024cm2
The smaller container has a volume of 1458cm3
Calculate the surface area of the smaller container.

 

[Saad the Paki]

Can someone help me out in this question please?? 0580/22/m/j/14 Question 18

The two containers are mathematically similar in shape.
The larger container has a volume of 3456cm3 and a surface area of 1024cm2
The smaller container has a volume of 1458cm3
Calculate the surface area of the smaller container.

First of all we nees to find the scale factor,k
This is done by taking the cube root of the volumes (3456/1458)
k will come out to be (4/3)
Now to find the area we have to sqaure (4/3) and divide 1024 by it

 

[Saad the Paki]

Can someone help me out in this question please?? 0580/22/m/j/14 Question 18

The two containers are mathematically similar in shape.
The larger container has a volume of 3456cm3 and a surface area of 1024cm2
The smaller container has a volume of 1458cm3
Calculate the surface area of the smaller container.

 

[Saad the Paki]

Anyone done with their english paper 2?

 

[misscute406]

Thank you so much man!! Saad the Paki and yeah for everyone exam begins tomorrow!! i mean english exam starts tomorrow for everyone!!! how will anyone have the papers??

 

[Saad the Paki]

No i meant like maybe other variants.. i think they happen on different days

 

[Lana19984]

5y = k.

Find 5^(y + 1) , in terms of k.
?????????????????????????????????