- Messages
- 764
- Reaction score
- 752
- Points
- 103
Thankooooooo!
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
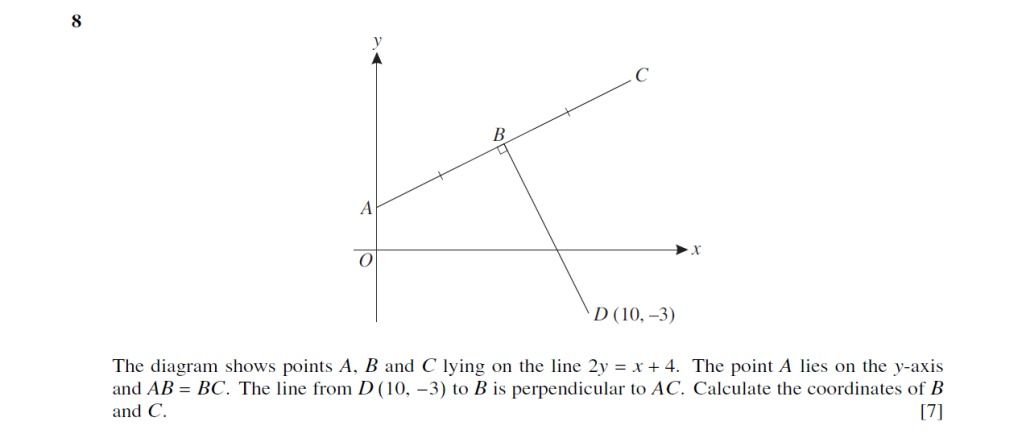
Hope u got it @sea_princess and @2paccan someone please solve question 8 : ii (b)
http://www.xtremepapers.com/papers/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_w10_qp_33.pdf

I have posted answer for O/N 2010 P33 Q8Hey,I also can't solve these kind of questions.Posted a question which had 2 theeta instead of 0.5 and sadly haven't gotten no response but its understandable as p1 examination is near.If you do at all get the answer for your query,please forward to me as well.
Thanks
Hello! Can you please try and solve my questions? They're above your replyI have posted answer for O/N 2010 P33 Q8
hope u'll be now able to solve the other question with 2 theeta if not
Reply me with the question and Paper no
Is that for any two lines or tangents?Oh that...Here is an example.
We have 2 lines with gradients m=2 and m=3 respectively.
To find the angle between them,
tan theta = 2
theta = 63.4
tan theta = 3
theta = 71.6
Angle between them = 71.6 - 63.4 = 8.2
YupIs that for any two lines or tangents?
Very helpful thank you
Are these from P1 ??Hello! Can you please try and solve my questions? They're above your reply
Thanks! Can you please try and solve my questions?


YesAre these from P1 ??
They're o/n 05 question 9 and m/j 09 queation 8Are these from P1 ??
thanx a lotHope u got it @sea_princess and @2pac
can someone please solve question 8 : ii (b)
http://www.xtremepapers.com/papers/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_w10_qp_33.pdf
Hey,I also can't solve these kind of questions.Posted a question which had 2 theeta instead of 0.5 and sadly haven't gotten no response but its understandable as p1 examination is near.If you do at all get the answer for your query,please forward to me as well.
Thanks
Hope u got it @sea_princess and @2pac
It's easy convert it into the general form
2(x^2 - 8x +10 )
2( (x)^2 -2(x)(4) + (4)^2 - (4)^2 + 10)
2( (x -4)^2 -16 + 10)
2(x-4)^2 -12
y = 2(x-4)^2 -12
y + 12/2 = (x-4)^2
underoot +-(y + 12)/2 +4 = x
F^-1(x) = +-(x + 12)/2 +4
Oops Sorry i misreadNo hard feelings but you've used the wrong range; albeit your answer is correct but the method isn't. The range which needs to be modified is '0 < θ < 360', not '0 < θ < 90'. The range '0 < θ < 90' is for 'a'.
I solved the second question thinking someone would solve the first and then we would have two identical solutions. (HappensThey're o/n 05 question 9 and m/j 09 queation 8
lol,was too confusing,ill have another look at it again and as for the 2 theeta question.I have posted answer for O/N 2010 P33 Q8
hope u'll be now able to solve the other question with 2 theeta if not
Reply me with the question and Paper no
Thank you very much! And unfortunately no one solved the other one =PI solved the second question thinking someone would solve the first and then we would have two identical solutions. (Happens)
For the second question,
i)
y=12/x --------1
y=-2x + 11 -------2
Set them equal and you get,
12/x = -2x + 11
2x^2 -11x + 12 = 0
Using the quadratic formula gives,
x = 4 , 3/2
y = 3 , 8
(4,3) (3/2,8)
ii) 12/x = -2x + k
Simplify to get 2x^2 - kx + 12 = 0
b^2 - 4ac < 0
k^2 - 4(2)(12) < 0
k^2 < 96
k < +√96
k > -√96
iii)
y=12x^-1
dy/dx= -12/x^2
At P, dy/dx = -12/(2)^2 = -3
tan theta = -3
theta = -71.6
For the line, tan theta = -2
theta = -63.4
Angle between them = -63.4-(-71.6) = 8.2
For more than 16 years, the site XtremePapers has been trying very hard to serve its users.
However, we are now struggling to cover its operational costs due to unforeseen circumstances. If we helped you in any way, kindly contribute and be the part of this effort. No act of kindness, no matter how small, is ever wasted.
Click here to Donate Now