Mathematics: Post your doubts here!

[syed1995]

Forgive me for the vague drawing. Look at the 4 Arrows which I have placed. They show you the trapezium.. Honestly you can simply do it with the rectangle - ( Area of sector + triangle)... I just mentioned the Trapezium because you said Rectangle - Sector.

To do this we need to find the angle COA first. Which is marked as red in the next drawing




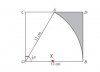
I will solve it with the Rectange method .. since it's both simle and easy to understand.

We need to find the Red Angle (COA)

COA = Pi/2 - Pi/3 = Pi/6

COA = Pi/6

Now We need to find the height and base of the triangle.

AC = 12 Sin (Pi/6) = 6 cm
OC = 12 Cos (Pi/6) = 6 √3


Area Of Rectangle = OB * OC = 12 * 6 √3
= 72 √3

Area Of Triangle = 1/2 * OC * AC = 1/2 * 6 * 6 √3
= 18 √3

Area Of Sector = 1/2 * r^2 * Angle AOB
= 1/2 * 12^2 * π/3
= 24 π

Shared Area= Area Of Rectangle - ( Area Of Unshaded Region) // Unshaded = Triangle + Sector

Therefore:
Rectangle - (Triangle + Sector)
=72 √3 - (18 √3 + 24 π)
=(72-18)√3 - 24 π
=54 (√3) - 24 π

a(√3) − bπ

a = 54 b = 24 Answer...

Also If we did the same with Trapezium .. then the height would be OC .. one side will be 12 .. other will be 12 - AC .. then find the area of trapezium with 1/2 * h * (Side 1 + Side 2)

= 1/2 * OC * (OB+AD)
= 1/2 * 6√3 * (12 + 6)
= 9 * 6√3
= 54√3

Area Of Trapezium - Area of Sector = Shaded

54√3 - 24π

same a = 54 b = 24

Check the answer and let me know if it's correct.

Hope this helps. Sorry again for the vague diagram and working .. I am not really good at explaining.

Cheers

 

[syed1995]

Thank you for your reply.. how come I don't see any trapezium there If possible, please help me identify it on the diagram.
Sorry for bothering..

The above was for you. Forgot to quote

 

[salvatore]

The above was for you. Forgot to quote

Thank you very very much for your help.. and you are gooooooood at explaining!

 

[sma786]

Salam,
I have my AS Level math mock paper on monday.
I'm very scared, please can anyone give me summarised notes for pure maths and statistics?
Thankyou!

 

[tanmaydube]

Summer 5 Q 7 ii) and Q8 ii)

Please help

 

[soumayya]

Summer 5 Q 7 ii) and Q8 ii)

Please help

Let f(x) = cosec x - 1/2 x - 1
f(0.5) = (1/sin 0.5 ) - 0.5(0.5) -1 =0.836
f(1) = (1/sin 1 ) - 0.5(1) -1 = -0.311

Since there is a sign change, a root lies between 0.5 and 1

 

[soumayya]

Summer 5 Q 7 ii) and Q8 ii)

Please help

 

[Iffat]

Ok, there definitely is a mistake. The position vector of R will be 9i+9j not minus. That's the only way you can solve this. If you doubt this just wait till your teacher confirms this.

a) PR = (9i+9j) - (i+3j) = 8i - 6j ; |PR|= 10
RQ = (9i+9j) -( 5i+11j) = 4i - 2j; |RQ| square root (20)
QP = (5i + 11j) - (i + 3j) = 4i + 8j; |QP| square root (80)
Use the Cos rule next.
Cos(theta) = (RQ^2+ QP^2- PR^2)/ 2*RQ*QP = (20+80 -10^2)/ 2* root 20* root 80 = 0
theta comes out as 90

b)PR/ |PR| = 8i-6j/ 10

c) (5i+ 11j) = m (i+3j) +n (9i+9j)
comparing two sides-
5= m +9n
11= 3m + 9n
solve and you get m=3 and n=2/9

Thanx u wer ryt it is plus ,
d photocopy i haf isnt clear

 

[sma786]

Can anyone give me a breif explanation of integration??

 

[tanmaydube]

Let f(x) = cosec x - 1/2 x - 1
f(0.5) = (1/sin 0.5 ) - 0.5(0.5) -1 =0.836
f(1) = (1/sin 1 ) - 0.5(1) -1 = -0.311

Since there is a sign change, a root lies between 0.5 and 1

Thanks a ton soumayya di!!!!!

 

[tanmaydube]

View attachment 21651

Cannot understand the 4 step clearly di,

it should be '4x+ln3' why is it '4x-ln3'

Thanks a lot again!

 

[Scafalon40]

http://papers.xtremepapers.com/CIE/...AS Level/Mathematics (9709)/9709_w02_qp_3.pdf
Q5 part (iii)
It's only worth one mark, could you tell me how to solve it?
n.b I'd prefer a method which is worth only one mark, as the question indicates
thanks a million!

 

[agarveer]

paper 32

nov 04 q 7

 

[tanmaydube]

Winter 5
Q 5, Q 6, Q10
Please help!!

Thanks a lot!

 

[Minato112]

Winter 5
Q 5, Q 6, Q10
Please help!!

Thanks a lot!

5) 8 sin θ − 6 cos θ = R sin(θ−α)
= R sin θ cos α - R cos θ sin α
Therefore,
R cos α = 8 ----- (1)
and R sin α = 6 ------ (2)

(1)^2 + (2)^2 => (R cos α)^2 + (R sin α)^2 = (8)^2 + (6)^2
=> R^2 [ (cos α)^2 + (sin α)^2 ] = 100 [ (cos α)^2 + (sin α)^2 ] = 1 (Identity)
Thus R^2 = 100
R = 10

(2) / (1) => tan α = (3/4)
α = *tan inverse* (3/4)
= 36.9○

8 sin θ − 6 cos θ = 10 sin(θ−36.9)
.......................................................

8 sin θ − 6 cos θ = 7
i.e 10 sin(θ−36.9) = 7
sin(θ−36.9) = 0.7
(θ−36.9) = *sin inverse* (0.7) = 44.4○
or (θ−36.9) = 180○ - *sin inverse* (0.7) = 135.6○

Therefore θ = 44.4○ + 36.9○ = 81.3○
or θ = 135.6○ + 36.9○ = 172.5○

--------------------------------------------------------------------------------------------------------------------

For the next 2 questions, if noone answers it, i'll answer it. I have to go for now. Hope it helps

 

[soumayya]

Cannot understand the 4 step clearly di,

it should be '4x+ln3' why is it '4x-ln3'

Thanks a lot again!

sorry...c is -1/4 ln 3
Hence it's (x - 1/4 ln 3)..the rest should B ok...

 

[littlecloud11]

Winter 5
Q 5, Q 6, Q10
Please help!!

Thanks a lot!

6i) x = sin^2 θ (Differentiate the right hand side with respect to θ)
dx = 2 Sin θ * Cos θ dθ
Now substitute x with Sin^2θ and dx with dθ in the left hand side of the eq. in the question and you get
∫√( Sin^2θ/ 1-Sin^2θ) * 2 Sin θ * Cos θ dθ
∫√(Sin^2θ/ Cos^2θ )* 2Sinθ * Cos θ dθ [1-Sin^2θ = Cos^2θ]
∫(Sinθ/Cosθ)* 2Sinθ * Cos θ dθ
Cancel out Cosθ and you get ∫2Sin^2θ dθ

ii) Cos2θ = 1- 2Sin^2θ
so re-write 2Sin^2θ as 1 -Cos2θ
You also have to change the limits. x = sin^2 θ so when x= 1/4, θ= π/6. When x= 0, θ =0
So, ∫2Sin^2θ dθ = ∫1- Cos2θ dθ
= [ θ - Sin2θ/2 ] upper limit π/6 and lower limit 0
Substitute the theta values and you get [{π/6 -Sin(π/3)/2 } - {0- Sin0}]
So the answer is π/6 - √3/4

 

[soumayya]

Winter 5
Q 5, Q 6, Q10
Please help!!

Thanks a lot!

 

[tanmaydube]

Thanks a lot soumayya, Minato112, littlecloud11 !!!!

 

[tanmaydube]

Minato112 bhai you will have to do the vector question (q 10) please!!!!!