which part?One more help please guys 9709 May/june 2009 P1 Q4 help please
-
We need your support!
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Mathematics: Post your doubts here!
- Thread starter XPFMember
- Start date
- Messages
- 7
- Reaction score
- 1
- Points
- 13
It wud be nice if u wud say which years question it issalam ....
can u plz tell me tat hw 2 expand a binomial having three terms? m really stuck hea !!! plz help me out
- Messages
- 7
- Reaction score
- 1
- Points
- 13
Both :'(which part?
part1) a represents amplitude i.e 6Both :'(
b represents number of cycles i.e 2
c represents the value of y from where the graph is starting i.e 3
part2) y = 6sin(2x) + 3Both :'(
at y = 0
0 = 6sin(2x) +3
6sin(2x) = -3
sin(2x) = -1/2
2x = sin inverse of (1/2) keeping the calc in radian mode
the value of sin is pie/6
it is -1/2 so sin -ve is in 3rd and 4th quadrant
so 2x = 7pie/6 or 11pie/6
x = 7pie/12 or 11pie/12
smallest value of x will be 7pie/12
- Messages
- 2
- Reaction score
- 0
- Points
- 1
lawwlz...It wud be nice if u wud say which years question it isor just the question and what the answer is supposed to be

Expand (1+x+2x(sq))(sq) check your answer with a numerical sustitution.
(sq) i used hea 2 denote square cz i dn noe hw 2 ri8 it using key board?
- Messages
- 165
- Reaction score
- 109
- Points
- 43
salam ....
can u plz tell me tat hw 2 expand a binomial having three terms? m really stuck hea !!! plz help me out
Please post that question.
- Messages
- 165
- Reaction score
- 109
- Points
- 43
lawwlz...Its frm P1( The course text book,nt d past paper) and it is as followz:
Expand (1+x+2x(sq))(sq) check your answer with a numerical sustitution.
(sq) i used hea 2 denote square cz i dn noe hw 2 ri8 it using key board?
(1+x+2x^2)^2
Suppose 'x+2x^2' to be one term.
[1 + (x+2x^2)]^2
Now expand the above equation.
[1 + (x+2x^2)]^2
1 + (x+2x^2)(2) + [(x+2x^2)^2(2)(1)]/2
1 + 2x + 4x^2 + (x+2x^2)^2
1 + 2x + 4x^2 + x^2 + 4x^3 + 4x^4
1 + 2x + 5x^2 + 4x^3 + 4x^4
Therefore, the final answer is '1 + 2x + 5x^2 + 4x^3 + 4x^4'.
- Messages
- 1,558
- Reaction score
- 2,428
- Points
- 273
Cud anyone please help me with q.3 paper 41 may june 2011? =(
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_s11_qp_41.pdf
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_s11_qp_41.pdf
- Messages
- 165
- Reaction score
- 109
- Points
- 43
Cud anyone please help me with q.3 paper 41 may june 2011? =(
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_s11_qp_41.pdf
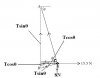
Refer to the above diagram and solve the horizontal and the vertical components of forces.
Horizontal Component:
T cos θ + T sin θ = 15.5
T cos θ = 15.5 - T sin θ
Vertical Component:
T cos θ + 8 = T sin θ
15.5 - T sin θ + 8 = T sin θ
23,5 = 2 T sin θ
11.75 = T sin θ
Therefore, T sin θ = 11.75~12
Put back this value of 'T sin θ' in the equation 'T cos θ = 15.5 - T sin θ'.
T cos θ = 15.5 - T sin θ
T cos θ = 15.5 - 12
T cos θ = 3.5.
Therefore, T cos θ = 3.5,
To find the value of θ, use the formula 'tan θ = opposite/adjacent'.
tan θ = opposite/adjacent
tan θ = (T sin θ) / (T cos θ)
tan θ = 12/3,5
θ = 73.73o
- Messages
- 1,558
- Reaction score
- 2,428
- Points
- 273
thankyou so muchHorizontal Component:
T cos θ + T sin θ = 15.5
T cos θ = 15.5 - T sin θ
Vertical Component:
T cos θ + 8 = T sin θ
15.5 - T sin θ + 8 = T sin θ
23,5 = 2 T sin θ
11.75 = T sin θ
Therefore, T sin θ = 11.75~12
Put back this value of 'T sin θ' in the equation 'T cos θ = 15.5 - T sin θ'.
T cos θ = 15.5 - T sin θ
T cos θ = 15.5 - 12
T cos θ = 3.5.
Therefore, T cos θ = 3.5,
To find the value of θ, use the formula 'tan θ = opposite/adjacent'.
tan θ = opposite/adjacent
tan θ = (T sin θ) / (T cos θ)
tan θ = 12/3,5
θ = 73.73o
XPFMember
XPRS Moderator
- Messages
- 4,555
- Reaction score
- 13,292
- Points
- 523
Assalamoalaikum wr wb!
Some more links added to the first post, and the old ones which weren't working have been fixed...
Some more links added to the first post, and the old ones which weren't working have been fixed...
Check this out! - Nice website, with video tutorials!
My P1 Notes! - Only few chapters available at the moment!
Maths Notes by destined007
Some Notes for P1 and P3 - shared by hamidali391
A LEVEL MATHS TOPIC WISE NOTES
MATHS A LEVEL LECTURES
compiled pastpapers p3 and p4 - by haseebriaz
Permutations and Combinations (my explanation)- P6
Permutations and Combinations - P6
Vectors - P3
Complex No. max/min IzI and arg(z) - P3
Range of a function. - P1
- Messages
- 60
- Reaction score
- 1
- Points
- 16
Thank you very much


- Messages
- 60
- Reaction score
- 1
- Points
- 16
THANK YOU VERY MUCHi m replacing theta with x
1/(2cosx +i - i2sinx +2 -i)
+i -i cancels out
1/(2cosx -i2sinx +2)
multiply and divide the whole fraction with the conjugate
[1/(2cosx + 2 - i2sinx)] * [(2cosx + 2 + i2sinx) / (2cosx + 2 + i2sinx)]
in the denominator: ( (2cosx + 2 + (2cosx + 2 + i2sinx) ) - i2sinx) * (2cosx + 2 + i2sinx)
taking (2cosx + 2) as a. and (i2sinx) as b. we apply the formula (a+b)(a-b) = a^2 - b^2; so
(2cosx + 2 + i2sinx) / {[(2cosx+2)^2] - [(i2sinx)^2]}
(2cosx + 2 + i2sinx) / {[4(cos^2)x + 8cosx + 4] + 4(sin^2)x}
-(i^2) is changed to +1 in the above step
4(cos^2)x + 4(sin^2)x is changed by identity [(cos^2)x +(sin^2)x = 1] to 4
(2cosx + 2 + i2sinx) / (8cosx + 8)
we jus have to prove the real part. so separate the real and imaginary part
(2cosx + 2) / (8cosx + 8)
(cosx + 1) / 4(cosx + 1)
cosx + 1 cancels out
1/4 is left which is constant for all values of theta
- Messages
- 60
- Reaction score
- 1
- Points
- 16
HELP NEEDED.
M/J/10.
P3
Q 4 (ii)
REPLY FAST.
I HAVE MY EXAM TOMORROW

M/J/10.
P3
Q 4 (ii)
REPLY FAST.
I HAVE MY EXAM TOMORROW
- Messages
- 60
- Reaction score
- 1
- Points
- 16
This is how we'll do this question:
1/(z+2-i)
We are given that ' z = 2 cos θ + i ( 1 - 2 sin θ )' so we'll put in this value of 'z' in the above equation.
1/(z+2-i)
1/[2 cos θ + i ( 1 - 2 sin θ )+2-i]
Arrange the real numbers and the imaginary numbers.
1/[(2 cos θ + 2) + i ( 1 - 2 sin θ -1 )]
1/[(2 cos θ + 2) - i ( 2 sin θ )]
THANKS ALOT
Next, multiply the equation '1/[(2 cos θ + 2) - i ( 2 sin θ )]' by the conjugate of '[(2 cos θ + 2) - i ( 2 sin θ )]'
{1/[(2 cos θ + 2) - i ( 2 sin θ )]} x [(2 cos θ + 2) - i ( 2 sin θ )] / [(2 cos θ + 2) + i ( 2 sin θ )]
[2 cos θ + 2 + i (2 sin θ)] / [(2 cos θ + 2)^2 + (4 sin^2 θ)]
As the question has asked us to deal with the real part only, we'll remove 'i (2 sin θ)' which is imaginary.
(2 cos θ + 2) / [(2 cos θ + 2)^2 + (4 sin^2 θ)]
(2 cos θ + 2) / (4 cos^2 θ + 8 cos θ + 4 + 4 sin^2 θ)
(2 cos θ + 2) / (4 cos^2 θ + 4 sin^2 θ + 8 cos θ + 4)
(2 cos θ + 2) / [4 (cos^2 θ + sin^2 θ) + 8 cos θ + 4]
Recall the identity 'cos^2 θ + sin^2 θ=1'.
(2 cos θ + 2) / [4 (cos^2 θ + sin^2 θ) + 8 cos θ + 4]
(2 cos θ + 2) / [4 (1) + 8 cos θ + 4]
(2 cos θ + 2) / (8 + 8 cos θ)
[2 ( cos θ + 1 ) ] / [ 8 ( 1 + cos θ ) ]
'cos θ + 1' cancels out as its present in both the numerator and the denominator. We are left with '2/8' now which further simplifies to '1/4'. Therefore, '1/4' is our final answer.
ur welcumTHANK YOU VERY MUCH
p31 or 32 or 33?HELP NEEDED.
M/J/10.
P3
Q 4 (ii)
REPLY FAST.
I HAVE MY EXAM TOMORROW

- Messages
- 118
- Reaction score
- 22
- Points
- 28
ur welcumthankyou soo much