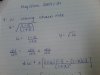Mathematics: Post your doubts here!

[saimaiftikhar92]

Q3(i):

y=6e^x - e^3x
(dy/dx) = 6e^x - 3e^2x
0 = 3e^x ( 2 - e^2x )
0 = 2 - e^2x
e^2x = 2
ln e^2x = ln 2
2x = ln 2
x= 0.35

Q3(ii):

(dy/dx) = 6e^x - 3e^2x
(d^2y/dx^2) = 6e^x - 9e^3x

Substitute the value of 'x=0/35' in the above equation which we've double differentiated. If the answer is negative, it's a maximum value. If the answer's positive, it's a minimum value.

(d^2y/dx^2) = 6e^x - 9e^3x

x=0.35

(d^2y/dx^2) = 6e^x - 9e^3x
(d^2y/dx^2) = 6e^(.35) - 9e^3(.35)
(d^2y/dx^2) = -16.97

As the answer is negative, this point is a 'maximum value'.

Q4:

( y )(dy/dx) = 1 + y^2
[( y )/(1+y^2)] dy = 1 dx

Integrate both the sides.

(1/2) ln (1+y^2) = x + c

Put 'y-2' and 'x=0' to find the value of 'c'.

(1/2) ln (1+y^2) = x + c
(1/2) ln 5 = c

Put back the value of 'c' into the integrated equation.

(1/2) ln (1+y^2) = x + (1/2) ln 5
(1/2) ln (1+y^2) - (1/2) ln 5 = x
(1/2) ln [(1+y^2)/5] = x
(1+y^2)/5 = e^2x
1+y^2 = 5e^2x
y^2 = 5e^2x -1

Therefore, the expression for y^2 in terms of 'x' is 'y^2 = 5e^2x -1'.

thankyou

 

[ffaadyy]

thankyou

You're welcome. Here's Q5:

Q5(i):


[√(1 + x) +√(1 − x)][
√(1 + x) −√(1 − x)]
(1 + x) + (1-x)(1+x) - (1-x)(1+x) - (1 - x)
(1 + x) - (1 - x)
2x

[√(1 + x) +√(1 − x)][
√(1 + x) −√(1 − x)] = 2x
[√(1 + x) +√(1 − x)] = 2x / [
√(1 + x) −√(1 − x)]

1 / [√(1 + x) +√(1 − x)]
1 / { 2x / [
√(1 + x) −√(1 − x)] }
[
√(1 + x) −√(1 − x)] / 2x

Q5(ii):

As '1 / [√(1 + x) +√(1 − x)]' is equal to '[
√(1 + x) −√(1 − x)] / 2x', we'll instead expand
'[
√(1 + x) −√(1 − x)] / 2x'.

[
√(1 + x) −√(1 − x)] / 2x

Expanding '√(1 + x) ':

√(1 + x) = 1 + (x/2) - (x^2)/8 + (x^3)/16

Expanding '√(1 − x)]':

√(1 - x) = 1 - (x/2) - (x^2)/8 - (x^3)/16

Putting the expanded variables back into the main equation.

[
√(1 + x) −√(1 − x)] / 2x
{[ 1 + (x/2) - (x^2)/8 + (x^3)/16 ] - [ 1 - (x/2) - (x^2)/8 - (x^3)/16 ] } / 2x

Open the brackets, do addition/subtraction of the like terms and then divide them by '2x' to obtain the final answer of:

(1/2) + (x^2)/16

 

[leadingguy]

please solve
question 6 part 2 of may/june 07 p3

 

[ffaadyy]

please solve
question 6 part 2 of may/june 07 p3

Simply plug in the values 'π/2' and '2π/3' in the place of 'x' in the equation 'x - 2 sin x'. One value will come out to be negative while as the other will come out to be positive if 'a' satisfies this equation.

x - 2 sin x

Put 'π/2' in the place of 'x'.

π/2 - 2 sin π/2
- 0.43

Now put '2π/3' in the place of 'x'.

2π/3 - 2 sin 2π/3
0.36

As one answer is negative and the other one is positive, 'a' satisfies this equation.

 

[leadingguy]

Simply plug in the values 'π/2' and '2π/3' in the place of 'x' in the equation 'x - 2 sin x'. One value will come out to be negative while as the other will come out to be positive if 'a' satisfies this equation.

x - 2 sin x

Put 'π/2' in the place of 'x'.

π/2 - 2 sin π/2
- 0.43

Now put '2π/3' in the place of 'x'.

2π/3 - 2 sin 2π/3
0.36

As one answer is negative and the other one is positive, 'a' satisfies this equation.

thanx !

 

[saimaiftikhar92]

i need help in this:
june 2007 question 3 and nov 2007 question no 1 and 2 of p3

 

[ffaadyy]

i need help in this:
june 2007 question 3 and nov 2007 question no 1 and 2 of p3

Q3, June 2007:

y = x sin 2x

x=π/4

Keep 'x=π/4' in the curve equation to find the value of 'y'.

y = x sin 2x
y = π/4 sin 2π/4
y = π/4

Differentiate the curve equation and then keep 'x=π/4' to find the value of the gradient

y = x sin 2x
(dy/dx) = sin 2x + 2x cos 2x
(dy/dx) = sin 2π/4 + 2 π/4 cos 2π/4
(dy/dx) = 1

Put back all these values in the equation of the tangent.

y - y1 = m (x - x1)
y - π/4 = 1 (x - π/4)
y = x

Therefore, the equation of the tangent is 'y = x'.

Q1, November 2007:

1/(2x-1) dx = 1

Integrate '
1/(2x-1)'.


1/(2x-1) dx = 1
(1/2) ln (2x - 1) = 1

Put the limits 'k' (upper limit) and '1' (lower limit).

(1/2) ln (2x - 1) = 1
(1/2) ln (2k - 1) - 0 = 1
ln (2k - 1) = 2
2k - 1 = e^2
2k = e^2 + 1
k = 4.19

Q2, November 2007:

Divide 'x^4 + 0x^3 + 3x^2 + 0x + a' by 'x^2 +x + 2' to find the value of a and also to find the other quadratic factor of p(x).

After the division, the value of 'a' will come out to be '4' while as the other quadratic factor will be 'x^2 - x + 2'.

 

[leadingguy]

i need help in this:
june 2007 question 3 and nov 2007 question no 1 and 2 of p3

june 07 p3 qstn 3


the equation of tangent to the curve is asked.
for that U need to find out co-ordinates of a point. jxt use the value of x ..(1/2pi) put it in eq. U will get the value of Y too.


now these values of x and Y will be ur coordinates

now differantiate the eq. of curve to get the gradient of that particular point.

note that the gradient of curve will be the gradient of the tangent as well.

for differantiating the eq. use product rule:

dy/dx= u.(dv/dx) + v.(du/dx) take u= x and v= sin2x

= x.2cos2x + sin2x.1

m = 2xcos2x + sin2x

now put value of x... (1/4pi) to get the gradient
U will get m = 1

now use the formula for finding eq. of line .......Y-y1 =m(X-x1) put values for Y1 , X1 and m

Y - (pi/4) = 1(X-(1/4pi))

solve it
U will get Y= X or Y= -X


this will be ur eq. of the tangent

hope U get it! ????

 

[saimaiftikhar92]

thankyou

 

[leadingguy]

i need help in this:
june 2007 question 3 and nov 2007 question no 1 and 2 of p3

question 1 p3 nov 07


frst simply integrate 1/(2x-1)

look that differential of 2x-1 = 2 , which can be achievable in numenator by multiplying the whole fraction by 1/2

i.e
1/2/(1/(2x-1)) integration will be
1/2[ln(2x-1)]
now put the boundries

1/2[ln(2(k)-1)] - 1/2[ln(2(1)-1)]

1/2[ln(2k-1)] - 1/2(ln1) =1

1/2[ln(2k-1)] - 0 = 1

ln(2k-1) = 1*2

ln(2k-1) = 2 now put the base "e" by removing ln

2k-1 = e^2
2k = e^2 +1

k = 4.19 ANS

 

[saimaiftikhar92]

AND QUESTION 2 OF NOV 2007 P3....

 

[1357913579]

iam not able to prove in mayjune 2010 paper-31 number-9 please have a look at what i have done and tell me where iam wrong and solve it to get the answer only for first part.
iam getting the answer as (1-x)^1/2 times by (1+x)^3/2 not able to get the same aswer required to be proved here is the attached files please reply as soon as possible.

 

[1357913579]

AND QUESTION 2 OF NOV 2007 P3....

here you go

 

[smzimran]

iam not able to prove in mayjune 2010 paper-31 number-9 please have a look at what i have done and tell me where iam wrong and solve it to get the answer only for first part.
iam getting the answer as (1-x)^1/2 times by (1+x)^3/2 not able to get the same aswer required to be proved here is the attached files please reply as soon as possible.

You are not wrong you just need to further simplify your answer...

 

[aksameerkhan27]

2cos2@ = 1
cos2@ = 0.5
new range is
0 ≤ 2@ ≤ 4pi

in one cycle (0 to 2pi), there are 2 positive values of 2@ (1st and 4th quadrant)
so, for 2 cycles(0 to 4pi), there will be 4 roots...

Thanx a lot

 

[aksameerkhan27]

Hi,
Pls help me in learning vectors in grade A2. can any one pls help me in all the necessary points to solve the vector questions in P3. Also need the checlist and important notes for vectors. Pls urgent.I am unable to understand the chapter.

 

[XPFMember]

Hi,
Pls help me in learning vectors in grade A2. can any one pls help me in all the necessary points to solve the vector questions in P3. Also need the checlist and important notes for vectors. Pls urgent.I am unable to understand the chapter.

assalamoalaikum wr wb!
check the first post of this thread..

 

[leadingguy]

june o7 question no. 9 part two! p3 I know that haw to apply formula and to get the angle .
but unfortunately m unable to get the other direction vector of the plane OAB


we are with the eq. of the plane ABC

how to get the other one?? to get both direction ratios


A detailed exlaination will be good!

 

[leadingguy]

june o7 p3 question 8 part 2

explain that how can we shade the region by the help of both inequalities???? M unable to use the enequalities given for shading the area.
a detalied explaination for the part will be good

 

[ffaadyy]

june o7 p3 question 8 part 2

explain that how can we shade the region by the help of both inequalities???? M unable to use the enequalities given for shading the area.
a detalied explaination for the part will be good

This's the diagram with the correct shading:



First of all, you'll construct a circle of radius '2' with centre at the origin (0,0). According to the inequality '|z|<2', area inside the circle will be shaded. Next, you'll construct a perpendicular bisector for the inequality '|z-u^2|<|z-u|'. Mark the complex numbers '-1,-1' (u) and '0+2i' (u^2) on the argand diagram. To construct a perpendicular bisector, place the compass on the point '-1,-1' , open it more than half and mark 2 arcs (one above and one below). Repeat the same procedure for the point '0+2i' and join both the arcs by a straight line (this line is the perpendicular bisector). Now comes the shading part. For the inequality '|z-u^2|<|z-u| , area above the perpendicular bisector will be shaded and according to the inequality '|z|<2', area inside the circle will be shaded. Therefore, the area which we'll be shading should be above the perpendicular bisector and inside the circle.

Also note that the circle and the perpendicular bisector are dotted lines, not solid lines. We can recognize whether it'll be a dotted line or a solid line by reading the inequality.