- Messages
- 1,394
- Reaction score
- 1,377
- Points
- 173
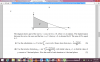
yaar!! mera answer positive nahi aaraha ! aafter taking the double derivative... negative araha hai!! ye keh rahi hoon main!did you get it cause i cannot get whats difficult and wat you are asking my friend. u need a psychiatrist
are you getting a positive answer?