- Messages
- 2,206
- Reaction score
- 2,824
- Points
- 273
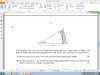
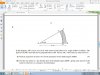
Let theta be x,
- PLZ HELP ME WITH THE QUESTION 5 !!
Part i)
sin^4x - cos^4x
= (sin^2x)(sin^2x) - (cos^2x)(cos^2x)
= (sin^2x)^2 - (cos^2x)^2
We know a^2 - b^2 = (a - b)(a + b)
= (sin^2x - cos^2x)(sin^2x + cos^2x)
We know sin^2x + cos^2x = 1
= (sin^2x - cos^2x)(1)
= sin^2x - cos^2x
sin^2x - cos^2x
= sin^2x - (1 - sin^2x)
= 2sin^2x - 1
Part ii)
sin^4x - cos^4x = 2sin^2x - 1
2sin^2x - 1 = 1/2
2sin^2x = 3/2
sin^2x = 3/4
sin(x) = (Roof of 3)/2
x = 60
As x lies between 0 to 360, there will be more 3 values of x.
x = 60 ; (180 - x) = (180 -60) = 120
x = 60 ; (x + 180) = (60 + 180) = 240
x = 120 ; (x +180) = (120 + 180) = 300
Therefore, x = 60, 120, 240, 300.