- Messages
- 54
- Reaction score
- 83
- Points
- 28
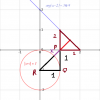
can somebody help me with this question
http://papers.xtremepapers.com/CIE/...S Level/Mathematics (9709)/9709_w13_qp_32.pdf
question 8b ???
http://papers.xtremepapers.com/CIE/...S Level/Mathematics (9709)/9709_w13_qp_32.pdf
question 8b ???