AS Level Pure Mathematics 1 Trigonometrywhich year is this? Just interested.
-
We need your support!
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Mathematics: Post your doubts here!
- Thread starter XPFMember
- Start date
Can u please explain again step by step? Its very confusing and it's on my head for almost around 2 weeks and I still haven't figured out how to solve these.Remember if the digits are odd, remove sin and and cos and vice versa, in case of tan, remove tan and add cot and vice versa.
Remember ASTC graph.
(a) sin(90 - theta) = 90 is odd so add cos remove sin. 90 - thetha = A so cos theta.
(b) sin (270+ theta) = 270 is odd so remove sin add cos, 270 + theta = C so sin is -ve = - cos theta.
(e) tan(-(180-theta)) = 180 is even, so no changes. tan(-theta) = tan theta.
REST TRY OUT YOURSELF, if u still have doubts, we are here to solve them.
- Messages
- 2,206
- Reaction score
- 2,824
- Points
- 273
http://sketchtoy.com/64898442Can u please explain again step by step? Its very confusing and it's on my head for almost around 2 weeks and I still haven't figured out how to solve these.
p1P1 or P3 ?
- Messages
- 2,206
- Reaction score
- 2,824
- Points
- 273
Is the answer one?
- Messages
- 1,826
- Reaction score
- 21,481
- Points
- 523
O/N/13 Paper 43.
Q1.
It says A particle moves upa line of greatest slope of a rough plane inclined at an angle alpha to the horizontal where sin alpha = 0.28. The coefficient of friction between the particle and plane is 1/3.
i) Show that the acceleration of the particle is -6.
Now, I checked the marking scheme and what they have done is something along the lines of -(mg)(cos alpha) - (mg sin alpha) = ma
I get how he resolves all but the symbols aint making sense to me. If the body is moving up, it should have a force in forward direction. But the component of weight and friction both acts backwards. So what is the forward force? And what is with the - signs?
This is how i pictured the question.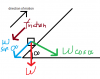
Q1.
It says A particle moves upa line of greatest slope of a rough plane inclined at an angle alpha to the horizontal where sin alpha = 0.28. The coefficient of friction between the particle and plane is 1/3.
i) Show that the acceleration of the particle is -6.
Now, I checked the marking scheme and what they have done is something along the lines of -(mg)(cos alpha) - (mg sin alpha) = ma
I get how he resolves all but the symbols aint making sense to me. If the body is moving up, it should have a force in forward direction. But the component of weight and friction both acts backwards. So what is the forward force? And what is with the - signs?
This is how i pictured the question.

What do u mean by 90 is odd and 180 is even?
I don't understand. Sorry but I truly didn't understand.
- Messages
- 2,206
- Reaction score
- 2,824
- Points
- 273
Oh c'mon man!What do u mean by 90 is odd and 180 is even?
I don't understand. Sorry but I truly didn't understand.
You dont know 90 is a odd number and 180 is a even number?
Sorry, I cannot make you explain more than I did.
- Messages
- 2,206
- Reaction score
- 2,824
- Points
- 273
Is the answer to that question 1?
90 is not an odd number its evenOh c'mon man!
You dont know 90 is a odd number and 180 is a even number?
Sorry, I cannot make you explain more than I did.
- Messages
- 924
- Reaction score
- 1,096
- Points
- 153
Good question.O/N/13 Paper 43.
Q1.
It says A particle moves upa line of greatest slope of a rough plane inclined at an angle alpha to the horizontal where sin alpha = 0.28. The coefficient of friction between the particle and plane is 1/3.
i) Show that the acceleration of the particle is -6.
Now, I checked the marking scheme and what they have done is something along the lines of -(mg)(cos alpha) - (mg sin alpha) = ma
I get how he resolves all but the symbols aint making sense to me. If the body is moving up, it should have a force in forward direction. But the component of weight and friction both acts backwards. So what is the forward force? And what is with the - signs?
This is how i pictured the question. View attachment 51871
Firstly, something moving in a certain direction does not necessarily mean there is a force pulling it in that same direction. This is because, everything moving continues to do so by default, if no force acts on it. (Newton's first Law I think).
As an example, think of a ball you throw vertically up. Yes, you did provide a force for a millisecond at first, but after that, the ball continues to go up on its own. The only force acting on it now is its weight caused by gravity, which acts downwards, but the ball is still moving up! So don't worry if something is moving up a slope without any force pulling it up, maybe someone pushed it. (in part 2 they tell you the initial push was 5.4 m/s in this question.)
As for the negative signs, before doing any mechanics question, you need to decide whether you want upward direction to be positive, or downward direction to be positive. Then the other direction becomes negative. Usually, people choose the direction of initial motion to be positive. Therefore, in this case, they chose the direction up the slope to be positive, and so all forces acting in this direction are positive. (in this case there aren't any). All forces acting downwards, is considered negative. (in this case both friction and weight component are to be considered negative) This is true not only for forces, but all vector quantities. (eg acceleration, velocity, displacement, etc will ALL be negative downwards, thus they told you to prove a = NEGATIVE six)
Anyhow, Fr = M*R (sorry cant do the greek letter mu)
Fr = 1/3 * R (1)
(Your diagram is missing R btw)
Resolving perpendicular to the plane:
R = Wcos(alpha)
(W is mg we know, cos(alpha) is sqrt(1-0.28^2) = 0.96)
R = 0.96*mg
Now we can find Fr:
Fr = 1/3 * 0.96 * mg
Fr = 0.32*m*g (and g = 10)
Fr = 3.2*m
We also need to know Wsin(alpha):
Wsin(alpha) = 0.28*m*g = 2.8*m
So applying Newton's Second Law:
Resultant force = ma
-Fr + -Wsin(alpha) = m*a
(you see, the forces are acting opposite to the positive direction we chose, so they are negative)
-3.2*m - 2.8*m = m*a
a = -6 ms^-2
Hope it's clear
Even I don't understand 0_O90 is not an odd number its even
- Messages
- 187
- Reaction score
- 191
- Points
- 53
9709/41/O/N/14
Q6 (ii)
You need two times. The first of which elapses for the ball falling in air before it reaches the liquids surface. The second of which elapses as it falls through the liquid.
The ball starts from rest, so u = 0.
For the first part the acceleration is +9.8 ms^-2, since we're considering down to be the positive direction in this case.
For the second part the acceleration is +5.5 ms^-2.
You have the distance covered in air, which is 5m.
The distance covered beneath the liquid surface is 4m.
For the first time, you can use the formula s = ut + 1/2 at^2
5 = 0xt + 1/2(9.8)(t^2)
5 = 4.9t^2
t^2 = 5/4.9
t = square root of 1.02
t = 1.01 which rounds up to 1.0 s.
Now you also need the final velocity, just before it hits the surface. They say there is NO instantaneous change in the velocity, so your final velocity in air will be the initial velocity in the liquid.
v^2 = (0)^2 + 2(9.8)(5)
v^2 = 98
v = 9.89 which rounds up to 10 ms^-1.
----------
For the second time and velocity, you can use v^2 = u^2 + 2as to get the velocity, and v = u + at to get the time.
First get your final velocity as the particle hits the bottom of the container. Remember, your initial velocity here will be the final velocity of the particle before it hit the surface, since they said there is no instantaneous change.
v^2 = (10)^2 + 2(5.5)(4)
v^2 = 144
v = 12 ms^-1
12 = 10 + 5.5(t)
2 = 5.5t
t = 0.36 s.
Now simply plot the graph like this,

You can confirm that the values are correct, by finding the area under the graph, Which should add up to 9m, which is the total distance covered by the particle in air and in the liquid.
Hope that helped
Attachments
Last edited:
- Messages
- 2,206
- Reaction score
- 2,824
- Points
- 273
IN 90 "9" is an odd number!!! in 180 "18" is even!!!!90 is not an odd number its even
- Messages
- 2,206
- Reaction score
- 2,824
- Points
- 273
CAN YOU TELL ME THE ANSWER OF THIS QUESTION?????
i donno frm what aspect r u calling it an even number however, overall 90 is an even number......IN 90 "9" is an odd number!!! in 180 "18" is even!!!!
