- Messages
- 140
- Reaction score
- 414
- Points
- 73
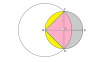
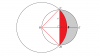
Hahaha ... That's what I'm talking about. Practice more and you will hopefully get it. Complex numbers and vectors also require a bit of imagination, or rather, visualisation.I dont find them that difficult, its just thinking a bit and that's all, but my marks goes only in this partsHence I am poor at it..
Anyways...