- Messages
- 39
- Reaction score
- 24
- Points
- 18
Anytime AmigoThanks Aheeta
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
Anytime AmigoThanks Aheeta
Nov08 7 , ii please
thanks a looootso let time at A be 0.
v = integration a dt
V= 10t - 0.15 (t^2) +c
at t=0 v=5 m/s
so V = 10t - 0.15 (t^2) +5
s = integration V dt
so S = 5(t^2) - 0.05(t^3) + 5t + c
at t=0 s=0
so S = 5(t^2) - 0.05(t^3) + 5t
for 3 s means that it has already travelled 1.25 m in 0.5 s
so t=2.5 s
at this time s=5(2.5^2) - 0.05(2.5^3) + 5(2.5)
so s= 43.0 m
so total distance fallen = 43.0 + 1.25 = 44.25 m
Aslkm...!!! what is the toughest paper m1 that exist.!?!
im stuck a bit in paper m1..mAybe bkoz im ruined
Hello there. I need help for this question:
View attachment 16613
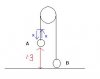
Thanks dear. But i don't get one thing. Look at this diagram:initial velocity of A = final velocity of B = 2.6 m/s
When string is slack a= 10m/s^2
at max height v = 0 m/s
(v^2) = (u^2) + 2as
0 = 6.76 + (2*-10*s)
S = 0.338 m
v = u + at
0 = 2.6 -10t
t = 0.26 s (time to reach max height)
therefore time to reach max height and return to equilibrium position = 0.26*2 = 0.52 s
distance travelled by B = 0.65 m
time taken to travel this distance = 0.5 s as calculated above in (ii)
therefore T = 0.5 + 0.52 = 1.02 s
So distance travelled by A in 0.5 s = 0.65 m
dist travelled by A in reaching the max height and returning back to the equilibrium position = (0.338*2) = 0.676 m
so total distance travelled in T s = 0.65 + 0.676 = 1.326 m
Use the equation s =ut + 0.5at^2 for both the particles and replace the values of "u" as given by the question and "a" as -10 ms^-2.
Thanks dear. But i don't get one thing. Look at this diagram:
View attachment 16620
Why is the distance here not (0.65 x 2), because i consider that both particles were initially at 0.65 on the ground, so when B slacks, A goes up 0.65 metres more, and is 1.3?
One more thing, can you explain me the part where it says "The string remains slack until A is at a height of 1.3 m above the ground for a second time"?
Does this mean, 2x (x + x) shown in the diagram above?
Okay got it. Thanks!so the first part:
this is because A was already 0.65 m above the ground. It only moves an additional 0.65 m, its height is 1.3 m but its displacement remains 0.65 m
second:
this implies the time when A is at first at 1.3 m above the ground i.e when B hits the ground
second time implies when A goes to a max height and returns back to its original position i.e at 1.3m , again above the ground
Hope it is ok now.
Using s = ut + (1/2)a(t^2)
sP = 12t - 5(t^2)
sQ = 7t - 5(t^2)
3 sP = 8 sQ
3{12t - 5(t^2)} = 8 {7t - 5(t^2)}
36t - 15t^2 = 56t - 40t^2
5t( 5t - 4) = 0
so t = 4/5 = 0.8 s
V=u+at
vP = 12 +(-10*0.8) = 4 m/s
vQ = 7 + (-10*0.8) = -1 m/s (travelling in the opposite direction)
Use the equation s =ut + 0.5at^2 for both the particles and replace the values of "u" as given by the question and "a" as -10 ms^-2.
For p:
Hp = 12t - 5t^2
For q:
Hq = 7t - 5t^2
Then use the equation given by question (i.e 3hp = 8hq ) and you will obtain the value of t. Then use the equation v = u + at to find out the velocities of each particles.
Hope this helps.
Rightly said! and i would add something, most importantly, thank them.People out here please develop a habit of hitting the "Like" button when someone helps you. It will encourage them to further help you when ever you need them. Will you loose anything by just hitting the like button when someone helps you? So please keep you ego aside and hit the "Like" button when someone helps you. Please try to appreciate the time they spent on helping you.

Yeah ! That's the main idea that I am trying to convey.Rightly said! and i would add something, most importantly, thank them.
For more than 16 years, the site XtremePapers has been trying very hard to serve its users.
However, we are now struggling to cover its operational costs due to unforeseen circumstances. If we helped you in any way, kindly contribute and be the part of this effort. No act of kindness, no matter how small, is ever wasted.
Click here to Donate Now