- Messages
- 12
- Reaction score
- 7
- Points
- 13
sagar65265
would you mind explaining me no. 7 ? :s
http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_s12_qp_42.pdf
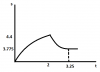
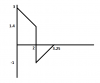
U can find acceleration by:
a = -0.12/0.15 = -0.8 (through F=ma)
So there is a negative acceleration, due to the resistive frictional force of 0.12N
at 2s the velocity is:
v = 3 + 2(-0.8) = 1.4 (through v=u + at)
KE after collision:
(0.5(0.15)(1.4)^2) - 0.072 = 0.075
Velocity after collision:
root(2*0.075/0.15) = -1 (the velocity is negative because the motion is opposite to the initial motion) (through K.E=0.5mv^2)
Frictional force remains the same, therefore deceleration is the same:
Therefore:
t= 2 + (1/0.8) = 3.25
U can do the displacement time graph through finding the area under the velocity-time graph......both are uploaded......