- Messages
- 69
- Reaction score
- 48
- Points
- 28
Can someone help me with this question, plzz?
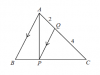
In the diagram, the points P and Q lie on the sides BC and AC of triangle ABC.
AB is parallel to QP.
AQ = 2 cm and QC = 4 cm.
The area of triangle CPQ is 6 cm2.
Find the area of
(a) triangle AQP [1]
(b) triangle ABC[1]
(c) triangle ABP [1]
(Its a nov 2012 paper 1 question)
In the diagram, the points P and Q lie on the sides BC and AC of triangle ABC.
AB is parallel to QP.
AQ = 2 cm and QC = 4 cm.
The area of triangle CPQ is 6 cm2.
Find the area of
(a) triangle AQP [1]
(b) triangle ABC[1]
(c) triangle ABP [1]
(Its a nov 2012 paper 1 question)
Attachments
Last edited: