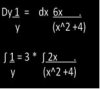- Messages
- 243
- Reaction score
- 198
- Points
- 43
Can any one please help me with this sum's part iv below please!
(I could do till iii but got badly stuck with part iv)
Q.The complex number −2 + i is denoted by u.
(i) Given that u is a root of the equation x
3 − 11x − k = 0, where k is real, find the value of k. [3]
(ii) Write down the other complex root of this equation. [1]
(iii) Find the modulus and argument of u. [2]
(iv) Sketch an Argand diagram showing the point representing u. Shade the region whose points
represent the complex numbers z satisfying both the inequalities
|z| < |z − 2| and 0 < arg(z − u) < 1/4π.
And please draw n upload the diagram here too...pleaaase i m really confused abt the diagram dat i should draw for part iv
Thank u! May u be blessed for helping!
BESIDES here is the mark scheme below... to me it sounded completely gibberish so i couldnot work out the last part of the sum!
(iv) Show point representing u in relatively correct position in an Argand diagram B1
Show vertical line through z = 1 B1
Show the correct half-lines from u of gradient zero and 1 B1
Shade the relevant region B1 [4]
[SR: For parts (i) and (ii) allow the following alternative method:State that the other complex root is –2 – i B1
State quadratic factor x2 + 4x + 5 B1
Divide cubic by 3-term quadratic, equate remainder to zero and solve for k, or, using
3-term quadratic, factorise cubic and obtain k M1
Obtain k = 20 A1]
please illustrate using a diagram!it all sounds gibberish when explained in words!