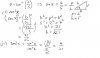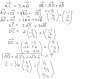Mathematics: Post your doubts here!

[abcde]

Q9) (i) Application of quotient rule:
y = (1 -x)/(1 + x)
=> dy/dx = [(1+x)(-1) - (1-x)] / (1+x)^2
=> dy/dx = - 2/ (1+x)^2

Now you can obtain an expression for dy/dx where y is the square-root of the original expression:
dy/dx = 1/2 [(1-x)/(1+x)]^-1/2 x -2/(1+x)^2
= -1/ (1+x)(1-x^2)^1/2
The gradient of the normal is -dx/dy so you get: (1+x)(1-x^2)^1/2

(ii) Let a = gradient of the normal = (1+x)(1-x^2)^1/2
=> da/dx = (-2x^2 - x + 1)/(1-x^2)^1/2
Equate this to 0 as the gradient has its maximum value at P.
The quadratic equation 2x^2 + x -1 = 0 is obtained, solving which yields the answers 1/2 and -1 (ignored).
So the x-coordinate of P is 1/2.
Hope this is the correct answer.

 

[saimaiftikhar92]

http://www.xtremepapers.com/CIE/index.p ... _qp_12.pdf

IN THIS QUESTION NUMBER 8 PART 2.......I NEED HELP IN IT

 

[talhajohar]

http://www.xtremepapers.com/CIE/index.php?dir=International%20A%20And%20AS%20Level/9709%20-%20Mathematics/&file=9709_s11_qp_12.pdf

IN THIS QUESTION NUMBER 8 PART 2.......I NEED HELP IN IT

 

[leosco1995]

Re: A level math question

Yes, it's technically a Physics question.

u = 21
a = 9.81
s = -1.5 (negative because it is downwards displacement)
t = ?

Using the formula s = ut + 0.5at^2,

-1.5 = 21t + 0.5(-9.81)(t^2)
4.91t^2 - 21t - 1.5 = 0

Solving this equation, you get 2 values. I didn't bother checking the negative one but the +ve one is 4.35s.

 

[jason234]

Re: Mathematics: Paper1 pure mathematics oct/nov 2006 Q2

Paper 1 pure mathematics oct/nov 2006 Q2 (i) and (ii)

 

[talhajohar]

this is one way of doing it

 

[saimaiftikhar92]

I NEED TO ASK A COUPLE OF MORE QUESTIONS :beer:



I NEED HELP IN :-

1) SHOW THAT THE EQUATION LOG (X+5)=5- LOG X CAB BE WRITTEN AS A QUADRATIC EQUATION IN X
2 2



2) THE PARAMETRIC EQUATION OF A CURVE ARE
X=Ln(TAN T) Y= SIN ^2 T WHERE 0 IS LESS THAN T IS LESS THAN 0.5 PIE
a) EXPRESS DY/DX IN TERMS OF T
b) FIND THE EQUATION OF THE TANGENT TO THE CURVE AT THE POINT WHERE X=0





3)TWO PLANES HAVE EQUATIONS X + 2Y -2Z=7 AND 2+Y+3Z=5

a)CACULATE THE ACUTE ANGLE BETWEEN THE PLANES
b)FIND A VECTOR EQUATION FOR THE LINE OF INTERSECTION OF THE PLANES

 

[talhajohar]

can you give the link of the question papers? that way it will be easier to understand.

 

[saimaiftikhar92]

http://www.xtremepapers.com/CIE/index.p ... _qp_32.pdf

IN IT QUESTION 2 , 5 AND 9

 

[jason234]

Im dead stuck on Q4 (ii) P1 O/N 2006

 

[saimaiftikhar92]

REPLY TO JASON:


FIRST FIND VECTOR AB WHICH IS b-a = (2 , -4 , 1)

then point c is such that vector ac = 3ab
VECTOR A + 3(AB)
VECTOR OC = ( -3, 6, 3) + 3(2, -4, 1) = (3, -6, 6)

THEN FIND THE MAGNITUDE OF VECTOR OC WHICH IS = 9


THEREFORE THE ANSWER WOULD BE 1/9(3 , -6 , 6)


HOPE I HELPED

 

[jason234]

p1 O/N 2006

Q6b (i) and (ii)

 

[talhajohar]

Im dead stuck on Q4 (ii) P1 O/N 2006

 

[Nibz]

^ You forgot to add the attachment!

 

[talhajohar]

yeah sorry

 

[saimaiftikhar92]

THE GEOMETRIC PROGRESSION IS AS FOLLOWS

144, X , 64 AND WE HAVE TO FIND THE VALUE OF X
FIRST OF ALL YOU HAVE TO FIND THE COMMON RATIO FOR WHICH YOU CAN FOLLOW THIS STEP

FIRST TERM IS R
SECOND IS AR
THIRD IS AR^2

SINCE A = 144 AND THIRD TERM IS 64
WE GET 144 r^2 = 64

r^2 = 64/144
r= 2/3
first term = 144 multiply by 2/3
=96
in second part just apply the formula for the sum to infinty

a/ 1-r

144 / 1-2/3
= 432

 

[saimaiftikhar92]

i have posted the link please help me in it

 

[talhajohar]

this is for 2 and 5

 

[jason234]

p1 o/n 2006 Q8 (ii) and (iii)

 

[talhajohar]

solution for q9