value of R is 5Thank you!!
btw wat abt the 3rd part of my other q?
for least value, we substitute the value [cos(theta + alpha)] with +1 and -1
so function will be 5(1) + 7 and 5(-1) + 7
so the least value is 2
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
value of R is 5Thank you!!
btw wat abt the 3rd part of my other q?
AoA!
AoA!
In part (a), you write this function as 5 sin (θ + 53.13).
So, 3 sin θ + 4 cos θ + 7 can be rewritten as 5 sin (θ + 53.13) + 7. The least value of this sin (θ + 53.13) part of the function is -1. Consequently, the least value of the entire function is = 5(-1) + 7 = 2.
You're welcome.Thank u!!
You're welcome.
@unique840: meine aap ka solution nai dekha tha. Honestly.
W.S!Asa, im stuck at question 2, maths P1 oct 2008
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_w08_ms_1.pdf
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_w08_qp_1.pdf
could u please explain it to me. Thank you.

It is about proving the identity?Asa, im stuck at question 2, maths P1 oct 2008
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_w08_ms_1.pdf
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_w08_qp_1.pdf
could u please explain it to me. Thank you.
Asa, im stuck at question 2, maths P1 oct 2008
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_w08_ms_1.pdf
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_w08_qp_1.pdf
could u please explain it to me. Thank you.
Can any help me to find out the Co-ordinate of D by vector method (Q no. 6 ii)
Question paper : http://www.xtremepapers.com/CIE/International%20A%20And%20AS%20Level/9709%20-%20Mathematics/9709_s07_qp_1.pdf
Marking Scheme : http://www.xtremepapers.com/CIE/International%20A%20And%20AS%20Level/9709%20-%20Mathematics/9709_s07_ms_1.pdf
May/June 2006 Question One :/ I don't understand the question.
1. A curve has equation y=k/x. Given that the gradient of the curve is -3 when x=2, find the value of the constant k. :/
AoA!Mechanics 1 Doubt
http://www.xtremepapers.com/CIE/index.php?dir=International A And AS Level/9709 - Mathematics/&file=9709_s10_qp_42.pdf
I got the concept but cannot find out the exact answer for Q4
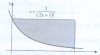
AoA!
Had some problems with integration!
- Find the area of the region enclosed by y = ( x - 2 ) ^ 4 and y = ( x - 2 ) ^ 3
- Draw the graph of the function f ( x ) when the graph of the inverse function f ' ( x ) is given ! http://www.mediafire.com/imageview.php?quickkey=sllcr94vcjmb0bz
- Find the area of shaded region View attachment 3503
For almost 10 years, the site XtremePapers has been trying very hard to serve its users.
However, we are now struggling to cover its operational costs due to unforeseen circumstances. If we helped you in any way, kindly contribute and be the part of this effort. No act of kindness, no matter how small, is ever wasted.
Click here to Donate Now