- Messages
- 1,594
- Reaction score
- 483
- Points
- 93
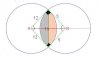
The line x=1 is clearly mentioned there.^No! The only thing given in the question was the equation of the curve i.e. y = 1 / (2x + 2) ^2 !
If you have that book, Pure Mathematics 1, you can see the question for yourself! Exercise 16 d, Question 5, part c !
Find the area under the curve using limits x=0 and x=1. Subtract this from the area of the entire rectangle.
Try solving it now. You can let us know if you still find it troublesome.