-
We need your support!
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Mathematics: Post your doubts here!
- Thread starter XPFMember
- Start date
- Messages
- 5,874
- Reaction score
- 4,242
- Points
- 323
thanks
- Messages
- 729
- Reaction score
- 477
- Points
- 73
Assalamualaikum,
This question is from P3 ,P2 and P3 book , Exercise 18A
Q.2) Intregation;(x-2)/(x-4)^1/2.dx
Thanks in advance for cooperation!
This question is from P3 ,P2 and P3 book , Exercise 18A
Q.2) Intregation;(x-2)/(x-4)^1/2.dx
Thanks in advance for cooperation!
Assalamualaikum,
This question is from P3 ,P2 and P3 book , Exercise 18A
Q.2) Intregation;(x-2)/(x-4)^1/2.dx
Thanks in advance for cooperation!
@mustehssun Iqbal: well, i need to do this... bcoz of unavailability of time, i wont be doin it.. i need to know what you will get when the lower part gets expanded.. anything it comes, i suggest you to do with partial fractions...by getting two individual terms or may be three..so that u can integrate easily..if u didnot get it, i will do it for you...
- Messages
- 165
- Reaction score
- 109
- Points
- 43
Assalamualaikum,
This question is from P3 ,P2 and P3 book , Exercise 18A
Q.2) Intregation;(x-2)/(x-4)^1/2.dx
Thanks in advance for cooperation!
@mustehssun Iqbal: well, i need to do this... bcoz of unavailability of time, i wont be doin it.. i need to know what you will get when the lower part gets expanded.. anything it comes, i suggest you to do with partial fractions...by getting two individual terms or may be three..so that u can integrate easily..if u didnot get it, i will do it for you...
Such questions in which you've to take a substitution yourself have never appeared in the previous maths paper 3's but still this's how you'll do it:
Take the substitution x -4 = (u)^2
x = (u)^2 + 4
dx = 2u du
Substitute the value of 'x' and 'dx' with 'x = (u)^2 + 4' and 'dx = 2u du' respectively in the equation '(x-2)/(x-4)^1/2 dx'
(x-2)/(x-4)^1/2 dx
{[(u)^2 + 4 - 2]/[(u)^2 + 4 - 4]^(1/2)} x 2u
{[(u)^2 + 2] / u} x 2u
2u^2 + 4
Now integrate this equation:
2u^2 + 4
[(2u^3)/3] + 4u
Replace 'u' with 'x' by substituting '(x - 4)^(1/2) = u' in this equation:
{ 2 [ ( x-4 )^1/2 ]^3} / 3 + 4 ( x-4)^1/2 + k.
Therefore, the answer is { 2 [ ( x-4 )^3/2 ] / 3 + 4 ( x-4)^1/2 + k.
- Messages
- 165
- Reaction score
- 109
- Points
- 43
what ansers u get for the 2nd part?
is the answer 10.4° and 61.2°?
- Messages
- 165
- Reaction score
- 109
- Points
- 43
last part?
In the 'ii' part, we'll construct a circle with center 1,2 and radius 2. Using that same diagram for the 'iii' part to find the greatest arg z, we'll draw a tangent to the circumference of the circle and make the x-axis our base line, like the one illustrated in this diagram (tangent and the base line indicated by the red colour):

Now to find the arg z, we'll use this diagram:
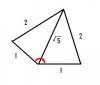
To find the angle, we'll simply do the following calculation:
tan θ = (2/1)
θ = 1.11 rad.
This angle is of one half only so we'll multiply it by '2' to obtain a final answer of '2.21 rad'.
- Messages
- 100
- Reaction score
- 72
- Points
- 38
Hello!
I need help in finding volume of revolution of a region enclosed by two curves.
Is it calculated by the same method we use for finding volume of rotation of a part of curve?
I need help in finding volume of revolution of a region enclosed by two curves.
Is it calculated by the same method we use for finding volume of rotation of a part of curve?
XPFMember
XPRS Moderator
- Messages
- 4,555
- Reaction score
- 13,292
- Points
- 523
Assalamoalaikum!
integrate => [g(x)]^2 - [f(x)]^2
square of equation of upper curve - square of lower curve...and integrate!
integrate => [g(x)]^2 - [f(x)]^2
square of equation of upper curve - square of lower curve...and integrate!
- Messages
- 1,833
- Reaction score
- 587
- Points
- 93
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_s04_qp_4.pdf
Q.7 need help. kindly explain in detail whichever formulas and ways u use in this ques. Thanks.
Q.7 need help. kindly explain in detail whichever formulas and ways u use in this ques. Thanks.
i) higher than the top of the tower means higher than 25 m.http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_s04_qp_4.pdf
Q.7 need help. kindly explain in detail whichever formulas and ways u use in this ques. Thanks.
from ground to top of tower means till 25 m, we hav the info as:
u = 30 m/s
v1 = ?
s = 25 m
a = -10
apply the formula
2as = v1^2 - u^2
2 (-10) (25) = v1^2 - (30)^2
v1 = 20 m/s
from top of tower to the maximum height the info is:
v1 = u
v2 = 0 (final velocity is zero at maximum height)
t = ?
a = -10
v = u + at
v2 = v1 + (-10)t
0 = 20 + (-10)t
t = 2 sec
total time = 2*2
= 4 sec
- Messages
- 106
- Reaction score
- 11
- Points
- 28
First of all, you'll simultaneously solve the curve equation and the line equation.
y = x^2
y = x + 2
x^2 = x + 2
x^2 - x - 2 = 0
x^2 - 2x +1x -2 = 0
x ( x - 2) + 1 (x - 2) =0
x = 2, x = -1
Now we have the x-coordinates of the point at which the curve meets the line. Accordingly, we'll find their y-coordinates which when calculated are y = 4 and y = 1.
So now we have two points, (2 , 4) and (-1 , 1). Next, we'll differentiate the curve equation 'y = x^2' to obtain the gradient function which is '(dy/dx) = 2x'. We'll insert the value x=2 in this equation to obtain a value of the gradient. The value of gradient is '4'. Inserting the values of y=4, x=2 and m=4 in the equation 'y - y1 = m (x - x1)', we get the first equation of the tangent which's 'y = 4x -4'. Similarly, using the other point which's (-1 , 1), we'll insert the value x = -1 in the gradient function to again obtain a value of the gradient which, for this point, comes out to be 'm = -2'. Again, we'll substitute the values of x = -1, y = 1 and m = -2 in the equation 'y - y1 = m (x - x1)' to obtain a second equation of the tangent which's 'y = -2x - 1'. Lastly, we'll solve both the equations of the tangents simultaneously to find their points of intersection.
-2x-1 = 4x-4
3=6x
.5=x
y=4x-4
y=4(.5)-4
y=-2
Therefore, the coordinates of the point of intersection of the tangents to the graph y=x^2 are ( .5 , -2 ).
Hey again.
But the question seems a lil different.
Find the equations of the tangents of the graph of y=x^2 AT THE POINT AT WHICH IT MEETS THE LINE WITH THE EQUATION y=x+2.
So Here they're asking us to find the point where it meets the line with equation y=x+2
the answer given is the same as yours but it doesn't satisfy the line eqn thing.
- Messages
- 165
- Reaction score
- 109
- Points
- 43
Hey again.
But the question seems a lil different.
Find the equations of the tangents of the graph of y=x^2 AT THE POINT AT WHICH IT MEETS THE LINE WITH THE EQUATION y=x+2.
So Here they're asking us to find the point where it meets the line with equation y=x+2
the answer given is the same as yours but it doesn't satisfy the line eqn thing.
We have to 'find the coordinates of the point of intersection of the tangents to the graph y=x^2 at the points at which it meets the line with equation y=x+2'. In simple words, the points at which the graph 'y=x^2' meets the line 'y=x+2', we have to find the 2 tangent equations at those points and then we'll solve both of those tangent equations simultaneously to find their points of intersection. This question is pretty easy to solve but a little tricky to understand.
- Messages
- 971
- Reaction score
- 532
- Points
- 103
find the coordinates of the point of intersection of the tangents to the graph y=x^2 at the points at which it meets the line with equation y=x+2.
The bolded part should make the question a lot more clear. When y=x^2 meets y = x + 2, it forms 2 equations. Both of them have a tangent. They want the equations of the intersection of the tangents. I agree the question might be a bit tricky to understand.
The bolded part should make the question a lot more clear. When y=x^2 meets y = x + 2, it forms 2 equations. Both of them have a tangent. They want the equations of the intersection of the tangents. I agree the question might be a bit tricky to understand.
- Messages
- 100
- Reaction score
- 72
- Points
- 38
Thankyou!Assalamoalaikum!
integrate => [g(x)]^2 - [f(x)]^2
square of equation of upper curve - square of lower curve...and integrate!