- Messages
- 1,824
- Reaction score
- 5,326
- Points
- 523
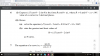
Oooooh okay, ryt!(ii) F = P/V
F ~ 1/V
Since the power is constant, the force is inversely proportional to V. In this situation, the acceleration will only be zero when the forward force will be equal to the resistive force. So in order to achieve this, the forward force must increase. As this will happen, the velocity of the car will decrease; therefore the velocity won't be a maximum when a=0 in this situation. Thus, this value of v is a minimum value here.
Thnx!!!!