-
We need your support!
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Mathematics: Post your doubts here!
- Thread starter XPFMember
- Start date
- Messages
- 924
- Reaction score
- 1,096
- Points
- 153
Edit! :
Once you have k=4/3, you can just proceed directly to tan-1(4/3) = 0.927
- Messages
- 135
- Reaction score
- 85
- Points
- 38
Thanks a ton!!!!!!!!
Edit! :
Once you have k=4/3, you can just proceed directly to tan-1(4/3) = 0.927
Oh ok, I didn't visualize it as being the equation of the line. Thanks.
Where did u disappear in last few days
Edit! :
Once you have k=4/3, you can just proceed directly to tan-1(4/3) = 0.927
- Messages
- 135
- Reaction score
- 85
- Points
- 38
- Messages
- 2,206
- Reaction score
- 2,824
- Points
- 273
- Messages
- 135
- Reaction score
- 85
- Points
- 38
- Messages
- 924
- Reaction score
- 1,096
- Points
- 153
- Messages
- 14
- Reaction score
- 8
- Points
- 13
Ohh got it! Thanks man.
How's ur prep overall? How is S1 going? What abt Physics and Chem?
60 - 70 %. Chemistry is OK. Math P3 needs some practice. I rock in Physics but I was never good in Statistics (S1 in this case) .
How about you?
- Messages
- 924
- Reaction score
- 1,096
- Points
- 153
Is this the entire question? Seems like it's missing something
- Messages
- 924
- Reaction score
- 1,096
- Points
- 153
Just brushing on my bio man :/Where did u disappear in last few days
- Messages
- 135
- Reaction score
- 85
- Points
- 38
y=-x+2-----Equation of line
How did you managed to get the other co-ordinates?
(2,0) And?
Thanks is advance...........
- Messages
- 924
- Reaction score
- 1,096
- Points
- 153
Consider arg(z) = 3/4*piy=-x+2-----Equation of line
How did you managed to get the other co-ordinates?
(2,0) And?
Thanks is advance...........
This represents the set of points whose argument is 3/4*pi. In other words, this is a line which makes the angle 3/4*pi radians with the x axes (in anticlockwise direction).
By doing tan(3/4*pi), we can find the gradient of the line, which is -1. So our equation is y=-x (passes through origin)
Changing arg(z) to arg(z-2) has the effect of shifting all the points to the right by 2 units, so now our equation becomes y=-x+2
- Messages
- 924
- Reaction score
- 1,096
- Points
- 153
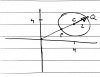
So basically you have a set of points that form a circle, with centre (4,4) and radius 2.View attachment 60475
b(ii) part
The distance from Origin to Centre = √(4²+4²) = 5.66
p = Ans - 2 = 3.66
q = Ans + 2 = 5.66
Attachments
- Messages
- 14
- Reaction score
- 8
- Points
- 13
So basically you have a set of points that form a circle, with centre (4,4) and radius 2.
The distance from Origin to Centre = √(4²+4²) = 5.66
p = Ans - 2 = 3.66
q = Ans + 2 = 5.66
Shouldn't it be √(6²+6²) for q and likewise for p?
And what about 'arg' part?
- Messages
- 924
- Reaction score
- 1,096
- Points
- 153
The questioner didn't ask about the arg part but if you want I'll do it tomorrowShouldn't it be √(6²+6²) for q and likewise for p?
And what about 'arg' part?
- Messages
- 135
- Reaction score
- 85
- Points
- 38
Consider arg(z) = 3/4*pi
This represents the set of points whose argument is 3/4*pi. In other words, this is a line which makes the angle 3/4*pi radians with the x axes (in anticlockwise direction).
By doing tan(3/4*pi), we can find the gradient of the line, which is -1. So our equation is y=-x (passes through origin)
Changing arg(z) to arg(z-2) has the effect of shifting all the points to the right by 2 units, so now our equation becomes y=-x+2
Wow!!!!!So basically you have a set of points that form a circle, with centre (4,4) and radius 2.
The distance from Origin to Centre = √(4²+4²) = 5.66
p = Ans - 2 = 3.66
q = Ans + 2 = 5.66
Thanks a bunch............