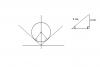
the circle is the locus (z-u) = 2Please Help !
November 2003 Maths P3 Question 7 (iii)
{z-(1+2i)}
means the coordinate will be 1,2 from where we will originate our locus
the line is the locus arg z
arg {z - (0+0i)}
means the coordinate will be 0,0 from where we will originate our locus
the greatest value of angle will be the angle between x-axis and the locus of arg z
it will be twice of theta...
find theta by the triangle and multiply it by 2 to find the greatest angle