- Messages
- 690
- Reaction score
- 321
- Points
- 73
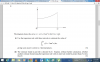
Well, with some help from the mark scheme, I can tell that the expression |z-2i| = zz* -2iz + 2iz + 4I´m actually looking for someone who can solve Q7(ii), the part of hence show that the modulus of z-2i = 4.
Here is the question once again:
Now if you look at it, its pretty similar to the expression already given in the question except that we have a positive 4, instead of -12.