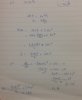- Messages
- 164
- Reaction score
- 193
- Points
- 53
Ohh my god ! .. I'm confused more now !
http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_w11_qp_13.pdf
Q9 (iii) part why is it (-5/2) <(or equal to) x < (or equal to) 0 ?
why it is not (-5/2) <(or equal to) x < (or equal to) (5/2)
Hadi Murtaza why are we talking about domain of f(x) and g(x) while we are dealing with gf(x) equation ? isn't it something else ? please explain what is related between all the 3 functions in the domain
Thought blocker If you can explain It will be helpful you know ..
f(x) and g(x) ARE related to each other by the function gf(x).
Solving (iii):
(2x+3)^2 - 6(2x+3)
= 4x^2 - 9 ≤ 16
= x^2 ≤ 25/4
x ≤ +/- 25/4
=> x ≤ +25/4 or x≤-25/4
The value of x must satisfy both the domains of g(x) and f(x)
Domain of g(x) is x must be less than or equal to 3, both +25/4 and -25/4 thus satisfy the domain of g(x)
However, the domain of f(x) is x must be less than or equal to 0. +25/4 obviously does not satisfy this domain and is therefore rejected.
=> -25/4 ≤ x ≤ 0
Hope that cleared things up.