- Messages
- 8,517
- Reaction score
- 34,844
- Points
- 698
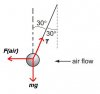
because since k is low for the first spring, the box will prevent it from breaking by over extending. Hence AI am sorry for bothering u again.. But could u explain this question to me??
http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Physics (9702)/9702_w10_qp_12.pdf