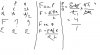Physics: Post your doubts here!

[Dr Death]

Hey, I have a question regarding Paper 5.
So in question 1, where a method of data analysis is required to be mentioned, the most common one is the graph.
Now, I know that it is mandatory to mention the variables plotted in the graph. But are we allowed to use derived variables?

I'll explain with an example...
S14 - Paper 51
The equation provided is T^2 = constant x (C-R)
where C and R are variables. The question asks us to investigate the relationship between T and R, for which I decided to draw a graph with (C-R) in the X axis and T^2 in the Y axis.

However, the marking scheme states that a graph of T^2 against R should be drawn. The analysis provided is also according to this. My analysis is different, for my graph is different.

I was wondering if, since my answer is different, would I gain the same credit as the answer in the marking scheme? Or would I not?

You may or may not get marks depending on the examiner. You are specifically asked to test the relationship between T and r. Not T and (c - r). You better get rid of the brackets and plot a graph of T^2 against R.

As y = mx + c, the equation can be rearranged so that you get : y = m * x + c
T^2 = constant * r + constant * C

Now your Y-Intercept = constant * c.
Gradient = constant

Y-Intercept / gradient = C.
So value of C can be determined..

Btw.. How did you manage to find the value of C ?

Hope this helps

 

[Dr Death]

is my displacement time graph for this situation okay?View attachment 51290View attachment 51291

Nope.
If that's a velocity time graph then yeah.. But displacement should increase rapidly at first, then comparatively slowly. Should not decrease

 

[Dream.Eater]

Can someone please explain these questions?
The answer is C in the first 2 and D in the last btw

 

[Dr Death]

View attachment 51303 View attachment 51304
View attachment 51305

Can someone please explain these questions?
The answer is C in the first 2 and D in the last btw

Young Modulus is same as material is same. Therefore as young's modulus = (f / a) * ( l /e). This can be used in both wires.

(60*l)/((d^2) * 8 ) = (60 * (l /4))/(((d^2)/4) * e)

where d = diameter
l = original length
e = extension to be found.

when you simplify above equation then you get e = 8 mm

 

[The Sarcastic Retard]

View attachment 51303 View attachment 51304

Can someone please explain these questions?
The answer is C in both btw

For other answer,
36:
A: k/2
B: k
C: 3k/2
D: 4k/3

 

[manya]

ITS A!
View attachment 51296

oh my god! thankyou so much. i dont know whats wrong with me

 

[The Sarcastic Retard]

View attachment 51303 View attachment 51304
View attachment 51305

Can someone please explain these questions?
The answer is C in the first 2 and D in the last btw

20:

 

[The Sarcastic Retard]

oh my god! thankyou so much. i dont know whats wrong with me

Nothing's wrong with you.

 

[Dream.Eater]

Young Modulus is same as material is same. Therefore as young's modulus = (f / a) * ( l /e). This can be used in both wires.

(60*l)/((d^2) * 8 ) = (60 * (l /4))/(((d^2)/4) * e)

where d = diameter
l = original length
e = extension to be found.

when you simplify above equation then you get e = 8 mm

Thanks!

 

[Dream.Eater]

20:View attachment 51306

Thanks!

 

[Dr Death]

 

[The Sarcastic Retard]

View attachment 51309

Look in the text book.
When the wire is stretched beyond its elastic limit, it will get permanently detached, that is, it won't return to original mean position.
The shapes of the graph need to be learnt.

 

[Dream.Eater]

Why is the answer D?

 

[Dr Death]

 

[Dream.Eater]

View attachment 51311

Its A since energy stored by stretching is always 0.5 * force * extension which is the area under the graph when taken graphically.

 

[Dr Death]

View attachment 51310

Why is the answer D?

The ball hits the wall with momentum of mu.
Momentum is a vector.

Lets consider "--->" to be positive. So the ball hits the wall with momentum mu.
If the ball rebounds with same speed then it is elastic collision as KE is conserved.

The resultant momentum has to be big enough to counteract the force AND send it flying back with momentum mu.

So taking -----> as positive, mu - 2 mu = - mu
so now that ball is traveling at a momentum mu towards left <------

 

[Dream.Eater]

The ball hits the wall with momentum of mu.
Momentum is a vector.

Lets consider "--->" to be positive. So the ball hits the wall with momentum mu.
If the ball rebounds with same speed then it is elastic collision as KE is conserved.

The resultant momentum has to be big enough to counteract the force AND send it flying back with momentum mu.

So taking -----> as positive, mu - 2 mu = - mu
so now that ball is traveling at a momentum mu towards left <------

But the answer is -2mu

 

[The Godfather]

View attachment 51310

Why is the answer D?

Change in momentum = Pf - Pi = -mu - mu = -2mu. Pf = -mu coz when the ball rebounds it travels in opposite direction.

 

[Dr Death]

But the answer is -2mu

Exaclty.
There is already a force of mu acting ---->
to stop the ball, momentum of mu acting <------- is needed.
To make the ball go with mu in <----- direction, further momentum of mu is needed.
mu + mu = 2mu <------ this way.
As momentum is vector, if -----> is +, then <----- is -.
So -2mu

 

[Dr Death]

How to add up spring constants?
(springs in series and parallel)