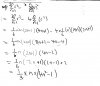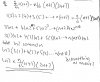Re: The Further Mathematics Thread. Post your doubts here!
I already appeared all my xams..and completed my A levels...but still...Since, i have interest in maths..i want to study Further mathematics....but...appearing xams later is not sure.....i wanna study just for fun....!! so some1 plz give me the link .....or any pdf file....like a book..so that i can study them...!!
I already appeared all my xams..and completed my A levels...but still...Since, i have interest in maths..i want to study Further mathematics....but...appearing xams later is not sure.....i wanna study just for fun....!! so some1 plz give me the link .....or any pdf file....like a book..so that i can study them...!!