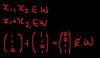- Messages
- 17
- Reaction score
- 0
- Points
- 1
Hmm, well, the first thing would be to express the new roots in terms of another variable; let's take y.
So, y= (x/x-2), no? Further, y= 1- (2/x-2).
Therefore, x= 2+ (2/1-y). Simply substitute this expression for x into the original equation- ie x^3 - 3x^2+1= 0, and expand. You should, I reckon, end up with the final expression. It's a painfully tedious expansion, but it should get you the right answer.
Yes, I got it! Thank you very much!