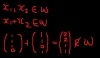Further Mathematics: Post your doubts here!

[guigao1994]

Hmm, well, the first thing would be to express the new roots in terms of another variable; let's take y.
So, y= (x/x-2), no? Further, y= 1- (2/x-2).
Therefore, x= 2+ (2/1-y). Simply substitute this expression for x into the original equation- ie x^3 - 3x^2+1= 0, and expand. You should, I reckon, end up with the final expression. It's a painfully tedious expansion, but it should get you the right answer.

Yes, I got it! Thank you very much!

 

[guigao1994]

Hello again everyone,

I have another doubt in the same paper... I understood what the first part of the question, but I don't know how to show that the vectors are linearly independent.
The rest of the question I have no clue.

Sorry for the long question!

Thank you very much!

 

[OakMoon!]

To prove that a set of vectors are linearly independent, you just have to show that they are not a linear combination of each other. To do that take the following example. Form an equation as shown.

For the 3 vectors not to be linearly related, the three parameters, a, b and c shoud be equal to 0. So just solve the above equation and you'll find out that a, b and c are equal to 0. Do the same for V2.

The second part is just a matter of observation. For V1 the 4th row has all elements=0 while for V2 the 3rd row has all elements=0 hence the vector containing both of these will be of the following form and you can then form the basis for V3

Btw, I have an advice for you. You need to cover the syllabus and understand the concepts from a teacher before you move on to past papers. You may be brave enough to try to do it all by yourself, but in Further Maths only past papers are not enough for complete understanding.
Secondly, instead of doing 02 papers, do the latest papers first. They have marking schemes which will make you understand the concept more easily. You can later do these old pps once you understand every concept.

 

[guigao1994]

To prove that a set of vectors are linearly independent, you just have to show that they are not a linear combination of each other. To do that take the following example. Form an equation as shown.
View attachment 5570
For the 3 vectors not to be linearly related, the three parameters, a, b and c shoud be equal to 0. So just solve the above equation and you'll find out that a, b and c are equal to 0. Do the same for V2.

The second part is just a matter of observation. For V1 the 4th row has all elements=0 while for V2 the 3rd row has all elements=0 hence the vector containing both of these will be of the following form and you can then form the basis for V3
View attachment 5572
Btw, I have an advice for you. You need to cover the syllabus and understand the concepts from a teacher before you move on to past papers. You may be brave enough to try to do it all by yourself, but in Further Maths only past papers are not enough for complete understanding.
Secondly, instead of doing 02 papers, do the latest papers first. They have marking schemes which will make you understand the concept more easily. You can later do these old pps once you understand every concept.

Thank you very much hamidali391!

I am struggling with the past papers because we have just finished the syllabus but we didn't have time to try questions, so although I know the content of the syllabus I still have problem when it comes to questions.

You are right, I will begin to do 07 onwards papers.

Just a last question: How would you do part (i) and (ii) of the question I posted?

Thank you very much again!

 

[OakMoon!]

Start from 11 and go backward. Secondly, it's useless to do the syllabus with a teacher and not practice questions with him/her. Btw, how could your teacher just do the syllabus with you and not practice questions? How could the teacher know that you grasped the concept or not? :S

i) Again, simple observation. W consists of either V1 OR V2. So two linearly independent vectors of W will have one vector with the 3rd row zero and one with the 4th row zero:

ii)For something to be a linear space it should obey some axioms. 1) It should contain the zero vector 2) It should be closed under addition, i.e if x1 and x2 belong to W then x1+x2 should also belong to W. But in this case the sum of the two vectors does not belong to W since each vector of W should have either it's 3rd row or 4th row as 0 which is not in this case.


This is the most simple question you'll find on Vector Spaces which proves that you are not aware of the simple concepts. So I'll advice you to revise your concepts.

 

[JuggyD]

The answers people have shared should be gathered together and listed for easy access. I think a link to this thread in the past papers section would be useful for people who aren't aware of the forums.

 

[OakMoon!]

There is a huge link on the main page for the forums. Secondly, this forum is only nine pages long, and it basically consists of questions. So you may just go through it.

 

[guigao1994]

Hey people,
I was doing a paper and dy/d(theta) appeared in the marking scheme to measure the largest distance of a polar curve from the initial line.
Could anyone tell me what else is it (dy/d(theta)) used for?

I know dx/d(theta) is used to find the tangents of a polar curve, but dy/dO is not mentioned in Further Pure Mathematics by Gaulter & Gaulter.
Thank you very much!

 

[OakMoon!]

Remember y=rsinΘ and x=rcosΘ. These are the basic equation to convert cartesian form to polar form or vice versa. That question that you came across asked for the maximum distance on the y axis. That is why you used dy/dΘ. If it was on x axis you would have similarly found the derivative of the equation connecting x to Θ. Hope this helps.

 

[JuggyD]

I found these through Google and thought they're pretty useful for some concepts.

 

[abcde]

^Nice!
I've found this website, which is just in accordance with our syllabus: http://www.stu.rdfz.cn/josephc/further.html.

 

[fhdaly]

MAY/june 2004 Q11 part (iv) VECTORS . Please advise, I am missing the concept by just 1%. Please explain stepwise, thank you.

 

[rama-x]

Re: The Further Maths Thread

Thank you, Nibz!
Here's the first problem:
If the roots of the equation x^4 - px^3 + qx^2 - pq x + 1 = 0 are α, ß, Γ and delta(D) show that:
( α + ß + Γ) ( α + ß + D) ( α + Γ + D) ( ß + Γ + D) = 1.

solution:

Let , S = α + ß + Γ + D= ( sum of the roots )=p

Therefore,
( α + ß + Γ) ( α + ß + D) ( α + Γ + D) ( ß + Γ + D)=( S-D) (S- Γ) (S- ß )(S-α )
=( p-D) (p- Γ) (p- ß )(p-α )
symmetric function,
let
y= p-x,
then substitute into the original equation,
x= p-y,

therefore,
(p-y)^4 - p(p-y)^3 + q(p-y)^2 - pq(p-y) + 1 = 0

y^4 - (3p)y^3 + (q^2+3p^2)y^2+(p^3+pq)y+1=0

the roots of this equation are
( p-D) , (p- Γ) , (p- ß ), (p-α )

then multiple of the roots,
( p-D) (p- Γ) (p- ß )(p-α ) =1.

There must be a better solution to this problem.

 

[abcde]

@MW24595: Here are the formulas used to calculate the x- and y-coordinates of the centroids of 2D/3D figures:

 

[Bhupendra Sharma]

join this facebook group... hopefully you will have access to some very cool stuffs for further mathematics
https://www.facebook.com/groups/ciefm/

 

[Bhupendra Sharma]

https://www.facebook.com/groups/ciefm/

 

[MW24595]

Hey, can anyone tell me what the simplest way to solve- May/June 2010 Paper 11 Question 6- ii)? I could re-expand but that gets annoyingly complicated and redundant. There seems to be some sort of equation to be found. How exactly does that happen?

 

[abcde]

Hey, can anyone tell me what the simplest way to solve- May/June 2010 Paper 11 Question 6- ii)? I could re-expand but that gets annoyingly complicated and redundant. There seems to be some sort of equation to be found. How exactly does that happen?

AoA! You don't have to make a single expansion. The equation in y can be re-written as S(n+6) + 2S(n+4) + S(n+2) - S( n) = 0. Taking n = 0, you get:
S(6) = -2(2) - (-2) + 3
[S( n) is 3 since the equation has 3 roots and the sum of each root raised to zero would give = 1+1+1 = 3]
=> S(6) = 1.
For S(8), take n = 2 this time.
If you're confused about the method I've used, refer to the 1st page of this thread.

 

[rama-x]

Hey, can anyone tell me what the simplest way to solve- May/June 2010 Paper 11 Question 6- ii)? I could re-expand but that gets annoyingly complicated and redundant. There seems to be some sort of equation to be found. How exactly does that happen?

 

[HM.RABBI]

Hey is it possible to give CIE further math in Oct/Nov-2012 session ?????