- Messages
- 138
- Reaction score
- 19
- Points
- 28
please I hope u will solve question 9)iii) nov qp 33 2011 mathematics A2 9709
but please as soon as possible because my exam is on 16 May
thanks
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
please I hope u will solve question 9)iii) nov qp 33 2011 mathematics A2 9709
but please as soon as possible because my exam is on 16 May
thanks
You sir,deserve a Trophy and a million likes.Whoaa that was a hectic task to write all that at MS Word :\
By the way here u go !!
Ahhh No problem !!You sir,deserve a Trophy and a million likes.
thanks a lot mate.
i)
Taking theta = x
a=x rads
a6= 4x rads
S6 = 6/2 (2(x) + 5d)
We know that S6 = 2pi
2pi = 6x + 15d ----1
a6 = a + 5d
4x = x + 5d
d=3x/5 ----2
Put 2 in 1 and you should get the value of x.
The perimeter of the smallest sector = rx + r + r

Yah thats my question , How can I do that?Find g-1(x) and replace x by 3.
Does anyone know how to differentiate this?Thanks

y=4-3sinxYah thats my question , How can I do that?
isnt this the question?Here's the answer
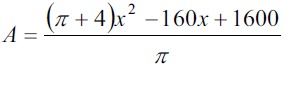
Ah man thats so simple! Lol tnx a lot!!y=4-3sinx
3sinx=4-y
sinx=4-y /3
x=sin-1(4-y/3)
g-1(3) = sin-1(4-3/3)
g-1(3) = 0.340
To find derivatives of equations like this one, its best to break it up.Does anyone know how to differentiate this?Thanks

okay correct me if I am wrong but AB=OB-OA right?Ahhh No problem !!
Prayers Needed
I gave the same answerTo find derivatives of equations like this one, its best to break it up.
A= [(pi x^2 +4x^2) / pi] - (160x/pi) + (1600/pi)
Simplifying further,
A = [ x^2 + {(4x^2)/pi}] - 160x/pi + 1600/pi
dA/dx = 2x + 8x/pi -160/pi
How do we get it in this form though?To find derivatives of equations like this one, its best to break it up.
A= [(pi x^2 +4x^2) / pi] - (160x/pi) + (1600/pi)
Simplifying further,
A = [ x^2 + {(4x^2)/pi}] - 160x/pi + 1600/pi
dA/dx = 2x + 8x/pi -160/pi
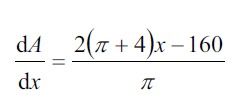
I think the 'long' method reduces the chances of errors because everything is kinda 'opened'. Plus, I am sure you've heard the saying "Old habits die hard".I gave the same answerBut I didn't simplify it
yours is long , just simply seperate 1/pi frn the equation and then find the derivative and put back 1/pi again

If the question asked you to get it in this form, then my method is not suitable. You should use the formal method just like Most_UniQue did.How do we get it in this form though?
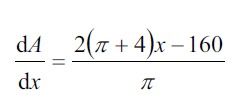
Thanks
For more than 16 years, the site XtremePapers has been trying very hard to serve its users.
However, we are now struggling to cover its operational costs due to unforeseen circumstances. If we helped you in any way, kindly contribute and be the part of this effort. No act of kindness, no matter how small, is ever wasted.
Click here to Donate Now