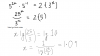- Messages
- 165
- Reaction score
- 109
- Points
- 43
I NEED HELP IN MAY JUNE 2010 /32 QUESTION NUMBER 7 AND 8
Q7(i).
(e^2t)(dx/dt) = cos^2 x
[1/(cos^2 x)] dx = (e^-2t) dt
(sec^2 x) dx = (e^-2t) dt
Integrate both the sides.
tan x = -(e^-2t)/2 + c
Put 'x=0' and 't=0' in the above equation in order to find the value of the constant 'c'.
tan x = -(e^-2t)/2 + c
0 = -1/2 + c
1/2 = c
Put back the value of 'c' in the integrated equation.
tan x = -(e^-2t)/2 + c
tan x = -(e^-2t)/2 + 1/2
tan x = 1/2 - (e^-2t)/2
x = tan^-1 [ 1/2 - (e^-2t)/2]
Therefore, the expression for 'x' in terms of 't' is 'x = tan^-1 [ 1/2 - (e^-2t)/2]'.
Q7(ii).
In differential equations where they ask us to 'state what happens to the value of [constant] when [constant] becomes very large', all what you need to do is keep the value of the number/expression which has a power with it to '0' and write down the remaining expression. For example in this equations case, x = tan^-1 [ 1/2 - (e^-2t)/2]', keep the value of '(e^-2t)/2' equal to '0' and state the left over expression which is 'tan^-1 (1/2)'.
Q7(iii).
Go back to the main equation and try arranging it in such a way that it becomes an expression for 'dx/dt' in terms of 't' and 'x'.
(e^2t)(dx/dt) = cos^2 x
(dx/dt) = cos^2 x/(e^2t)
(dx/dt) = (cos^2 x)(e^-2t)
The derivative is 'positive' that's why x increases as t increases.
Q8(i).
z = (1 + cos 2x) + i (sin 2x)
Finding the modulus of 'z'.
|z|:
√(1 + cos 2x)^2 + (sin 2x)^2
√(1 + 2 cos 2x + cos^2 2x + sin^2 2x)
Recall the identities 'cos 2x = 2 cos^2 x - 1' and 'sin 2x = 2 sin x cos x'.
cos 2x = 2 cos^2 x - 1
cos^2 2x = (2 cos^2 x - 1)^2
cos^2 2x = 4 cos^4 x - 4 cos^2 x + 1
sin 2x = 2 sin x cos x
sin^2 2x = 4 sin^2 x cos^2 x
sin^2 2x = 4 cos^2 x ( 1 - cos^2 x )
sin^2 2x = 4 cos^2 x - 4 cos^4 x
Replace 'cos^2 2x' with '4 cos^4 x - 4 cos^2 x + 1' and 'sin^2 2x' with '4 cos^2 x - 4 cos^4 x '.
√(1 + 2 cos 2x + cos^2 2x + sin^2 2x)
√(1 + 2 (2 cos^2 x - 1) + 4 cos^4 x - 4 cos^2 x + 1 + 4 cos^2 x - 4 cos^4 x)
√(1 + 4 cos^2 x - 2 + 4 cos^4 x - 4 cos^2 x + 1 + 4 cos^2 x - 4 cos^4 x)
√4 cos^2 x
2 cos x
Therefore, |z| = 2 cos x.
Argument:
tan x = b/a
tan x = (sin 2x)/(1 + cos 2x)
tan x = (2 sin x cos x)/(1 + 2 cos^2 x - 1)
tan x = sin x / cos x
tan x = tan x
Q8(ii).
1/z
[1/((1 + cos 2x) + i (sin 2x)] x [(1 + cos 2x) - i (sin 2x)]/[(1 + cos 2x) - i (sin 2x)]
(1 + cos 2x)/[(1 + cos 2x)^(2) + sin^2 2x]
'(1 + cos 2x)^(2) + sin^2 2x' is equal to '4 cos^2 x' as found in the first part.
(1 + cos 2x)/[(1 + cos 2x)^(2) + sin^2 2x]
(1 + cos 2x)/(4 cos^2 x)
(1 + 2 cos^2 x - 1)/(4 cos^2 x)
1/2