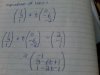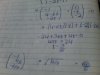Mathematics: Post your doubts here!

[ffaadyy]

can someone please explain how to solve question 9 :may/june 2010-paper 3(variant 1)

Q10(i).

(dA/dt) = k [(4/3)πr^3]

(dA/dt) = (dr/dt) x (dA/dr)

A = 4πr^2
(dA/dr) = 8πr

(dr/dt) = 2

(dA/dt) = (dr/dt) x (dA/dr)
(dA/dt) = (2) x (8πr)
(dA/dt) = 16πr

(dA/dt) = k [(4/3)πr^3]
(dr/dt) x (dA/dr) = k [(4/3)πr^3]
16πr = k [(4/3)πr^3]

Substitute '5' in the place of 'r' in the above equation to calculate the value of the constant 'k'.

16πr = k [(4/3)πr^3]
80π = k [500π/3]
0.48 = k

Substitute the value of 'k' back in the main equation.

(dr/dt) x (dA/dr) = k [(4/3)πr^3]
(dr/dt) x ( 8πr ) = (0.48) [(4/3)πr^3]
(dr/dt) = (1.92/24)πr^2]
(dr/dt) = 0.08πr^2

Q10(ii).

(dr/dt) = 0.08r^2
(1/r^2) dr = 0.08 dt

Integrate both the sides.

- (1/r) = 0.08t + c

Substitute '5' and '0' in places of 'r' and 't' respectively to calculate the value of the constant 'c'.

- (1/r) = 0.08t + c
- (1/5) = c

Put the value of 'c' back in the integrated equation.

- (1/r) = 0.08t + c
- (1/r) = 0.08t - (1/5)
- (1/r) = - [ -0.08t + (1/5) ]
1/r = -0.08t + (1/5)
1/r = (1/5) - 0.08t
(5/r) = 1 - 0.4
5/(1-0.4) = r

Therefore, an expression for 'r' in terms of 't' is 'r = 5/(1-0.4)'.

 

[sea_princess]

(dA/dt) = k [(4/3)πr^3]

(dA/dt) = (dr/dt) x (dA/dr)

A = 4πr^2
(dA/dr) = 8πr

(dr/dt) = 2

(dA/dt) = (dr/dt) x (dA/dr)
(dA/dt) = (2) x (8πr)
(dA/dt) = 16πr

(dA/dt) = k [(4/3)πr^3]
(dr/dt) x (dA/dr) = k [(4/3)πr^3]
16πr = k [(4/3)πr^3]

Substitute '5' in the place of 'r' in the above equation to calculate the value of the constant 'k'.

16πr = k [(4/3)πr^3]
80π = k [500π/3]
0.48 = k

Substitute the value of 'k' back in the main equation.

(dr/dt) x (dA/dr) = k [(4/3)πr^3]
(dr/dt) x ( 8πr ) = (0.48) [(4/3)πr^3]
(dr/dt) = (1.92/24)πr^2]
(dr/dt) = 0.08πr^2

actually this is not the question, this is the one I mean

 

[ffaadyy]

actually this is not the question, this is the one I mean

The attached file has a question from June 2010 while as, above, you had asked for a question from November 2009.

 

[sea_princess]

I asked for both
but I got what's wrong with the 2009 question now. thanx a lot

 

[Chooi1993]

T

Please view the attached .pdf file, the scanned solution of Q10's inside it.

Thanks a lot !

 

[saimaiftikhar92]

please help me in june 2006 q 7 p3

 

[ffaadyy]

please help me in june 2006 q 7 p3

Q7(i).

u = 2 + i
u* = 2 - i
u + u * = 2 + 1 + 2 - i = 4 + 0i

Mark the points O (0,o), A (2,1), B (2,-1) and C (4,0) on an argand diagram and join all the points. The resulting shape will be Parallelogram with adjacent sides equal.

Q7(ii).

u/u*

(2 + i)/(2 - i)
[(2 + i)/(2 - i)] x [(2 + i)/(2 + i)]
[(2+i)^2]/5]
(4 + 4i - 1)/5
(3 + 4i)/5
(3/5) + (4i/5)

Q7(iii).

arg u/u* = 2 arg u

arg u/u*:

tan^-1 (4/5)/(3/5)
tan^-1 (4/3)

arg u:

tan^-1 (1/2)

arg u* = 2 arg u
tan^-1 (4/3) = 2 tan^-1 (1/2)

 

[Chaitanya Agrawal]

Can you give a level maths papers 9709 for october 2011 for papers 12,32,42 and 62?

 

[leadingguy]

help needed in
june 2011 paper 3 varient 1 question 3

 

[ffaadyy]

help needed in
june 2011 paper 3 varient 1 question 3

AB = OB - OA
AB = (2)(-2)(11) - (-1)(2)(5)
AB = (3)(-4)(6)

'(3)(-4)(6)' is the direction of the plane.

3x - 4y + 6z = k

The plane passes through 'b' therefore you can find the value of 'k' using the coordinates of 'b'.

3x - 4y + 6z = k
3(2) - 4(-2) + 6(11) = k
80 = k

Put back the value 'k' in the plane equation.

3x - 4y + 6z = k
3x - 4y + 6z = 80

Therefore, the plane equation is '3x - 4y + 6z = 80'.

 

[1357913579]

i have a doubt in vectors iam getting wrong answer it from the cie book though i think it would be easy for you guys but iam getting wrong answer below i have attached the question as well as the what i have solved correct answer written in the back of the book 69^1/2 /13 means 69 under square root divided by 13
please reply asap

 

[ffaadyy]

i have a doubt in vectors iam getting wrong answer it from the cie book though i think it would be easy for you guys but iam getting wrong answer below i have attached the question as well as the what i have solved correct answer written in the back of the book 69^1/2 /13 means 69 under square root divided by 13
please reply asap

I am getting the same answer i.e '5/13'. Answers written at the back of the book are incorrect sometimes.

 

[1357913579]

oh ok thanks wait a minute i have another question of same sort iam uploading now just have a look at it becuase even this case iam getting different answer compared to the book

 

[smzimran]

i have a doubt in vectors iam getting wrong answer it from the cie book though i think it would be easy for you guys but iam getting wrong answer below i have attached the question as well as the what i have solved correct answer written in the back of the book 69^1/2 /13 means 69 under square root divided by 13
please reply asap

I am getting the same answer i.e '5/13'. Answers written at the back of the book are incorrect sometimes.

Me too, same answer iam getting!

 

[1357913579]

here is the other question i mentioned

 

[smzimran]

here is the other question i mentioned

Your method seems to be correct in this one also..
Which book is this BTW ?

 

[1357913579]

cie endorsed puremathematics 2 and 3 hugneill and douglas quading

 

[ffaadyy]

here is the other question i mentioned

I am getting the same answer as yours but the answer listed at the back of the book is [21(15)^(1/2)]/5]

 

[smzimran]

cie endorsed puremathematics 2 and 3 hugneill and douglas quading

I am getting the same answer as yours but the answer listed at the back of the book is [21(15)^(1/2)]/5]

The answer given in this part might also be wrong...

 

[Albert Einstein]

November 2004 paper 3 no 9 third part........9709...nidd it quickly