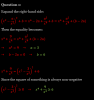- Messages
- 260
- Reaction score
- 104
- Points
- 53
In i, Why do we need two points that are on both planes?
We need two points because we need to find the line's vector. The fastest way to find the vector is to obtain two points on the line.
If you are interested in another method of determining the vector, you can use the normal vectors of P1 and P2.
If the vector is parallel to both planes, then it must be perpendicular to both planes' normal vectors, n1 and n2
Thus you can use cross product, n1 x n2, the product is the parallel-to-both-planes vector we are looking for.
Also couldn't it be that the planes were skewed?
In a 3-dimension space, only lines can be skewed to each other. Planes can only be parallel or intersecting.