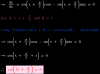- Messages
- 8,516
- Reaction score
- 34,844
- Points
- 698
Sure
YEEES please do!
I suggest solving pastpaper questions maybe? We don't get the explanation of the answers always,
especially things like stats and mechanics.