- Messages
- 24
- Reaction score
- 13
- Points
- 3
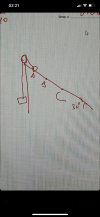
I didnt know thats how you get the phase shift. I first sketched the graph of y=csc(2x) and then shifted it pi units to the right (y=csc(2x-pi)) is this wrong? I've been doing this for a long time and always got the right answers.do the same for the other equation csc(2x)