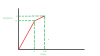
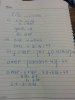It's not too bad as long as you understand that the v/t graph is the graph of the gradient of s/t and remember a few cases.Do u know how to convert a velocity time graph to distance time or vice versa? I'm rly facing issue in this
constant velocity is a straight diagonal line for displacement
straight diagonal line for velocity is increasing gradient graph for displacement
curved graph for velocity is increasing gradient at an increasing/decreasing rate for displacement, depending on the curve in the v/t graph
Because we are doing definite integration. The c cancels out.I have some doubts please clear.
- Why is 'c' ignored when integrating velocity to find disp?
There is no 'right' or 'wrong' direction. Positive can be any direction as long as you show motion in the opposite direction as negative.Won't they cut marks if I drew it in the wrong direction?