-
We need your support!
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Maths, Addmaths and Statistics: Post your doubts here!
- Thread starter OakMoon!
- Start date
- Messages
- 785
- Reaction score
- 2,290
- Points
- 253
you are Wrong here! I presumeView attachment 38071
i dunnoi just typed the answer
View attachment 38071
i) just find the area of this shaded cylindrical region
ii) 1 cubic cm = 1 ml
and 25000 l = 25000000 ml
so time taken for 1 ml (cubic cm) to come out = 1 sec
thus time taken for 25000000 ml = 25000000/(Volume u found in 'i')
- Messages
- 785
- Reaction score
- 2,290
- Points
- 253
Wait!!!okil see
Bi is still nt clear by d way
- Messages
- 785
- Reaction score
- 2,290
- Points
- 253
okil see
Bi is still nt clear by d way
(i) Formulae here is = Pi*Speed*Square of Radius
So, in this case
Pi =Moslty 3.142, but Varies Calculator to Calculator
Speed = 300cm/s as given
Sqaure of Radius = 4.5 * 4.5 = 20.25
hence we have, 3.142 (Pi) x 300 (Speed) x 20.25 (Sqaure of Radius)= 19087.65cm/s
Lets Simplyfy =19088 cm/s or 19.1 liters
Whats Confusing?
- Messages
- 785
- Reaction score
- 2,290
- Points
- 253
No, You are right in Seconds, just convert to minsyou are Wrong here! I presume
- Messages
- 785
- Reaction score
- 2,290
- Points
- 253
I said Pi * Speed * Raduis^2okil see
Bi is still nt clear by d way
3.142 * 300 * 4.5 ^2=
3.142 * 300 * 20.25 = 19100 Cm^3
Paen kera software haiView attachment 38071
i dunnoi just typed the answer
View attachment 38071
i) just find the area of this shaded cylindrical region
ii) 1 cubic cm = 1 ml
and 25000 l = 25000000 ml
so time taken for 1 ml (cubic cm) to come out = 1 sec
thus time taken for 25000000 ml = 25000000/(Volume u found in 'i')
- Messages
- 785
- Reaction score
- 2,290
- Points
- 253
I never understand, what is so confusing in this? ZohaKhan
software?Paen kera software hai
u really got that?got uSorry sorry

- Messages
- 785
- Reaction score
- 2,290
- Points
- 253
Oh! Finally, Useless me came Usefullgot uSorry sorry

- Messages
- 308
- Reaction score
- 625
- Points
- 103
as we know thatCan someone tell me how to do Q25
(a)the area under the speed-time graph is the distance traveled by the object.

so in first 20 seconds the car travels D meters. that means, 0.5 * u * 20 = D (by applying the formula for area of a triangle.
10u = D
for the time after '20 seconds' we need to find when does the car travels another D meters.
so t * u = D
t * u = 10u
so we divide both sides of equation by u and we get, t = 10
thus 2D meters are traveled in 20 + 10 = 30 seconds
(b)
acceleration from 0 to 20 seconds = (u-0)/(20-0) = u/20
thus if we change acceleration to deceleration (negative acceleration: in which the speed slows down) we just change its sign i.e.
(-u/20) * 0.5 (coz Q says deceleration was half of it) = -u/40
so according to the formula acc = v/t
we get t = v/acc by dividing both sides by acc and then multiplying them with t.
so t = 60 + [(u/4) - u] / -u/40
where [u/4] - u = velocity change from 60 seconds to t seconds
hope you got it
- Messages
- 61
- Reaction score
- 70
- Points
- 28
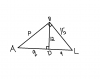
for any pair of triangles, u should take:For two similar triangles like these how do I determine the unknown sides? Tha angle at B is a right angle and so is ADB a right angle
AD= q cm
AB=p cm
AL= q+9 cm
BL=15 cm
BD=12 cm
DL=9 cm
please reply fast
View attachment 38213
base : base
hypotenuse : hypotenuse
height : height
all i mean to say is, u should take ratios of corresponding sides.
as hyp (hypotenuse) is always the side opposite to right angle
so we take the ratio p : (9 + q)
the smaller side of each triangle...
12 : 15
longer side making the right angle...
q : p
we deduce
12/15 = p/(9+q) ----------> 1
12/15 = q/p -----------> 2
solve the 2 simultaneous equations and u'll get ur answer
- Messages
- 61
- Reaction score
- 70
- Points
- 28
thanks man
- Messages
- 785
- Reaction score
- 2,290
- Points
- 253
lolX! Man I got it atleastas we know that
(a)
View attachment 38210
so in first 20 seconds the car travels D meters. that means, 0.5 * u * 20 = D (by applying the formula for area of a triangle.
10u = D
for the time after '20 seconds' we need to find when does the car travels another D meters.
so t * u = D
t * u = 10u
so we divide both sides of equation by u and we get, t = 10
thus 2D meters are traveled in 20 + 10 = 30 seconds
(b)
acceleration from 0 to 20 seconds = (u-0)/(20-0) = u/20
thus if we change acceleration to deceleration (negative acceleration: in which the speed slows down) we just change its sign i.e.
(-u/20) * 0.5 (coz Q says deceleration was half of it) = -u/40
so according to the formula acc = v/t
we get t = v/acc by dividing both sides by acc and then multiplying them with t.
so t = 60 + [(u/4) - u] / -u/40
where [u/4] - u = velocity change from 60 seconds to t seconds
hope you got it
- Messages
- 308
- Reaction score
- 625
- Points
- 103
as we know that
(a)
View attachment 38210
so in first 20 seconds the car travels D meters. that means, 0.5 * u * 20 = D (by applying the formula for area of a triangle.
10u = D
for the time after '20 seconds' we need to find when does the car travels another D meters.
so t * u = D
t * u = 10u
so we divide both sides of equation by u and we get, t = 10
thus 2D meters are traveled in 20 + 10 = 30 seconds
(b)
acceleration from 0 to 20 seconds = (u-0)/(20-0) = u/20
thus if we change acceleration to deceleration (negative acceleration: in which the speed slows down) we just change its sign i.e.
(-u/20) * 0.5 (coz Q says deceleration was half of it) = -u/40
so according to the formula acc = v/t
we get t = v/acc by dividing both sides by acc and then multiplying them with t.
so t = 60 + [(u/4) - u] / -u/40
where [u/4] - u = velocity change from 60 seconds to t seconds
hope you got it
Thanks!