- Messages
- 2,222
- Reaction score
- 4,914
- Points
- 273
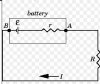
For finding what the gradient gives us u should look at the values on y and x axis as the formula of gradient is rise/run meaning (value on y axis/value on x axis) e.g if the graph has force on y axis and area on x axis the formula of pressure can come in our mind as P=F/A so we can say gradient gives the pressure......u need to know all the formulae that can make graphs easy :|I really need some guidance about the graphs the gradient of which graph gives what? The area under which graph gives what? and all such details. I'd be greatfull if someone could kindly help me out. asma tareen usama321 Thought blocker