Physics: Post your doubts here!

[asd]

I guess yeah
well, not the series part.

 

[cyclone94]

cyclone94..
View attachment 24771

thnku sooooooooooooooooooooooooooooooo much bro.......

 

[asd]

gary221 Ammeter is in parallel
We're not even using it to measure the current in the wire. :|

 

[Sapphires]

http://papers.xtremepapers.com/CIE/...nd AS Level/Physics (9702)/9702_s11_qp_41.pdf
Can someone please explain question 10c (ii) and 11b?
In question 10 c ii, why do we multiply x (thickness) by 2?
Thank you so, so much.

 

[ahmed abdulla]

http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Physics (9702)/9702_w07_qp_2.pdf
q 5a plz !
..... i always get confused with phase and path differnce and stuff ... any explaination on how to draw them ,,, ???

 

[gary221]

http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Physics (9702)/9702_w07_qp_2.pdf
q 5a plz !
..... i always get confused with phase and path differnce and stuff ... any explaination on how to draw them ,,, ???

u mean only the phase diff???
its easier if u convert the angle in radian ie multiply by (π/180°) ----> 60° = π/3 rads.
n c this --->
thts whr the new wave will start!

 

[ahmed abdulla]

u mean only the phase diff???
its easier if u convert the angle in radian ie multiply by (π/180°) ----> 60° = π/3 rads.
n c this ---> View attachment 24783
thts whr the new wave will start!

thanks##
can you please draw it with caliperating the amplitude and the phase differnce ... because i want to make sure .. and my teacher didnt explain this topic well!

pi/3 rad will be on left ??? wouldnt it

 

[gary221]

thanks##
can you please draw it with caliperating the amplitude and the phase differnce ... because i want to make sure .. and my teacher didnt explain this topic well!

pi/3 rad will be on left ??? wouldnt it

oh yes ofc..m bad!

hold on!

 

[ahmed abdulla]

oh yes ofc..m bad!

hold on!

i think u slept
caN you draw it again .. with everything caliperated>??Ashique

 

[gary221]

i think u slept
caN you draw it again .. with everything caliperated>??Ashique

i didnt!!
its soo diff to draw a graph on paint.. on a laptop!!
not my fault!!
nywy, i think it'll b sth like this...

 

[ahmed abdulla]

i didnt!!
its soo diff to draw a graph on paint.. on a laptop!!
not my fault!!
nywy, i think it'll b sth like this...
View attachment 24790

thanks ... next time dont sleep ... gn

 

[gary221]

thanks ... next time dont sleep ... gn

achaw??
-_-

 

[syed1995]

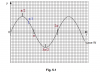
Phase difference always got to me as well
Anyhow
Phase difference=[(distance between the two waves on the x-axis)/(period of either one of the waves] *360 (or 2pi of you want to work with radians. I prefer degrees, and the question is in degrees as well).

So they already told us phase diff. which was 60 degrees. We can count the number of small boxes to know the period. The number of small boxes is 30 for one whole wave.
so putting everything into our formula
60= (distance between the waves)/30 * 360
60/360= (distance between the two waves/30)
1/6= distance between the two waves/30
distance between the two waves 1/6 * 30
=5.

So now we know the distance between the two waves is going to be 5 small boxes. And the period is going to be the same (30 small boxes). So you need to start the wave 5 small boxes from the original wave. and the period will be the same.
I simplified it a bit for you! Hope you wont get confused any more

You cleared a very big concept for me. Thanks man

 

[ahmed abdulla]

You cleared a very big concept for me. Thanks man

he is a good guy and deserve all the best !

 

[ahmed abdulla]

Ashique gary221 i ve gone throught all phase differnce questions and was able to do almost all of them ... all that because of allah's help and then you thanks !!

last question and i hope i am not annoying you bro !!
qn 6 (b) and (c) i and iv ..... isnt it 90 degree ? in MS it shows zero rad! what does the sign in last question mean
http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Physics (9702)/9702_s11_qp_23.pdf

 

[Sapphires]

As for question 11 b
(i) The amplitude for the sinusoidal signal would remain unchanged since the question mentions it is being modulated by FREQUENCY and not amplitude. So the amplitude would remain 5V
(ii) and (iii) Now, the carrier wave has frequency deviation of the carrier wave is 20 kHz V^-1. This means that for every 1 V change in the signal, the frequency of the carrier wave changes by 20 kHz. Now the carrier wave has an amplitude of 2V. So shift produced by the signal is 2*20= +- 40
So max frequency is 600+40= 640 kHz and min frequency is 600-40= 560 kHz
(iv) Since the carrier wave has a frequency of 7kHz, the change every second of the modulated wave is going to 7000.

Thank you! Your explanation was very clear.

 

[Nidz-Ahmed]

http://papers.xtremepapers.com/CIE/...and AS Level/Physics (9702)/9702_s06_qp_2.pdf 2 a(ii )

 

[Nidz-Ahmed]

Length of AC=2/3 AB
Moment of W about A= 2/3(AB) * W (clockwise)
Moment of P about A= (AB) * Tsin(beta) (anti-clockwise)
2/3(AB)W = (AB)Tsin(beta)
2/3W = Tsin(beta)

Thanks Alot

 

[goodluckayesha]

http://papers.xtremepapers.com/CIE/...and AS Level/Physics (9702)/9702_w05_qp_2.pdf
http://papers.xtremepapers.com/CIE/...and AS Level/Physics (9702)/9702_w05_ms_2.pdf
umm... plz explain question 5 part ci n cii as im unable to understand them from the mark scheme part cii can be done by ratio method too but I cant work it out so plz help with it

 

[Tkp]

http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Physics (9702)/9702_w05_qp_2.pdf
http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Physics (9702)/9702_w05_ms_2.pdf
umm... plz explain question 5 part ci n cii as im unable to understand them from the mark scheme part cii can be done by ratio method too but I cant work it out so plz help with it

5ci)i1/i2=(a1/a2) ^2
1/i2=(9/4)
i2=4/9