- Messages
- 129
- Reaction score
- 306
- Points
- 73
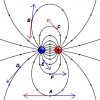
I don't understand question 35. May someone please explain it?
http://papers.xtremepapers.com/CIE/...nd AS Level/Physics (9702)/9702_w12_qp_13.pdf
http://papers.xtremepapers.com/CIE/...nd AS Level/Physics (9702)/9702_w12_qp_13.pdf