- Messages
- 100
- Reaction score
- 89
- Points
- 38
mmmm why cant 3^y=-3/4
Q4 ii) MAT/JUNE 2011/31
Because to calculate y you'll need to calculate ln(-3/4)/ln(3) & ln(-ve number) is never possible!
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
mmmm why cant 3^y=-3/4
Q4 ii) MAT/JUNE 2011/31
thanksalready did it here man...
http://www.xtremepapers.com/communi...st-your-doubts-here.9599/page-127#post-228526
help needed in q6 ii
12 × 27^y + 25 × 9^y − 4 × 3^y − 12 = 0
One of the factors is 2x^2 − 3x + 3hey can anyone show & explain the complete working for q5(ii) that will earn all 3 marks in http://www.xtremepapers.com/papers/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_w08_qp_3.pdf ??
thanks...
(http://www.xtremepapers.com/papers/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_w08_ms_3.pdf
&
http://www.xtremepapers.com/papers/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_w08_er.pdf)
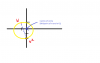
Post the whole question with link to the p.p and m.s !how do we solve this z^6=-64
https://docs.google.com/viewer?a=v&...ufarCv&sig=AHIEtbR25jP8EKBUeSdXW_ilg8B8yTawGwPost the whole question with link to the p.p and m.s !
I think this is a question from complex numbers.
Next time post the link to the m.s as well!Can anyone explain to me why q10 (ii) answer is 1800 ?Please help me ! 2moro is my exam !How to get the initial value ?
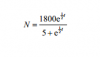
Its simple:
thanks a bunchIts simple:
Break the power 6 into 3 times square and solve for both roots one by one
Like this:
(− root(3) + i)^2 * (− root(3) + i)^2 * (− root(3) + i)^2
Btw, are you a teacher ?
View attachment 9581
w = -1 + i
w^2 = 0 - 2i
To find centre of circle, use midpoint formula:
= [ {(-1 + 0) / 2} , {(i - 2i) / 2} ]
= [-0.5 , -0.5i ]
To find radius find half the length of w to w^2
= 0.5 * | {-1 - (0)} , {i - (-2i)} |
= 0.5 * | -1 , 3i |
Find length by taking modulus
radius = 0.5 * root [ (-1)^2 + (3)^2 ]
= 0.5 * root [1 + 9]
= 0.5 * root (10)
Now write the equation in the form |z − (a + bi)| = k
where (a + bi) is the coordinate of the centre of the circle
and k is the radius
http://www.xtremepapers.com/CIE/International A And AS Level/9709 - Mathematics/9709_s04_qp_3.pdf
Q6..
ive reached till this point..dunno how to continue..
ln y + (y^3/3) = x +(1/3)
Please help!!
For almost 10 years, the site XtremePapers has been trying very hard to serve its users.
However, we are now struggling to cover its operational costs due to unforeseen circumstances. If we helped you in any way, kindly contribute and be the part of this effort. No act of kindness, no matter how small, is ever wasted.
Click here to Donate Now