-
We need your support!
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Mathematics: Post your doubts here!
- Thread starter XPFMember
- Start date
- Messages
- 227
- Reaction score
- 571
- Points
- 103
View attachment 23414
The answer to the first part is 1/x + 10/x^2 + 1/(10-x)
Cannot do part (ii) please help!
Okay, the first thing to notice is that they've given you the rate of change of x with respect to t in terms of x; this is not a very easy form to work with,
it's like writing dy/dx in terms of y. What you can do now is take the reciprocal of each side; it is proved that
dx/dy = 1/(dy/dx)
so you can take the reciprocal on each side and write
dt/dx = 100/x^2(10-x)
so this is more useful, since this equation now tells us how t changes with respect to x in terms of x. Another thing about this new form is that it is now the same equation as the one they asked you to split up into partial fractions in part (i), so you can substitute the values you have obtained earlier:
dt/dx = 1/x + 10/x^2 + 1/(10-x)
now you have an integral that can be carried out more easily than the earlier one. Multiplying both sides by dx,
dt = 1/x + 10/x^2 + 1/(10-x) dx
This you can integrate to give
t = ln(x) - 10/x - ln(10-x) + k ------- (1)
This constant is still an issue, so substitute the given values :- t = 0 and x = 1 to obtain:
0 = 0 - 10 - ln(9) + k
10 + ln(9) = k
So you can plug this value of k back in your equation (1) to get
t = ln(x) - 10/x - ln(10-x) + 10 + ln(9)
And using the properties of logarithms ( ln(a) + ln(b) = ln(ab) and ln(a) - ln(b) = ln(a/b) )
t = ln((9 times x)/(10-x)) - 10/x + 10
t = ln(9x/(10-x)) - 10/x + 10
which is the answer in the marking scheme.
Hope this helped!
Note: Before multiplying both sides by dx, make sure that you have separated out the variables in the equation, i.e. all terms in t must be on the left side and all terms in x must be on the right side, because it may not be possible to integrate t in terms of x or vice versa; separate the terms to the correct side and integrate both sides to get a differential equation with the constant.
Good Luck!
No problemthanks alot aleezay
- Messages
- 154
- Reaction score
- 88
- Points
- 38
http://papers.xtremepapers.com/CIE/...S Level/Mathematics (9709)/9709_s12_qp_42.pdf
Can anybody please help me with question 4 part ii)?
Can anybody please help me with question 4 part ii)?
- Messages
- 6,232
- Reaction score
- 5,004
- Points
- 573
To everyone posting their questions please... Include the link of the papers so as to facilitate the task of the ones solving it. Thnx 
- Messages
- 869
- Reaction score
- 374
- Points
- 73
in part i we got v= 40 + Tsin25 and x= Tcos25http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_s12_qp_42.pdf
Can anybody please help me with question 4 part ii)?
we have been told that the system is in equilibrium so this means the frictional force (F) will be equal to horizontal component (x) of the tension and we know the equation F = μR
R is the contact force which is the force that the rod is acting on ring which is 40 + Tsin25
substitute these in our equation and we will get:
T cos25 = 0.4(40 + T sin25)
T cos 25 = 16 + 0.4T sin25
T cos25 - 0.4T sin25 = 16
T = 16/(cos 25-0.4sin25)
T= 21.7 N...thats it!
i hope u got it
http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_w09_qp_61.pdf
Q5 b(ii) why we are taking 11C+11C3 instead of 8C5+8C3 wont it be the same then if the question asked for random selection
and can someone plz explain Q6 also
Q5 b(ii) why we are taking 11C+11C3 instead of 8C5+8C3 wont it be the same then if the question asked for random selection
and can someone plz explain Q6 also
- Messages
- 381
- Reaction score
- 140
- Points
- 53
in Q5bii) it says that either the male cousins will be selected or they will not it doesnt specify about the boys that are left so they must be included in the equationhttp://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_w09_qp_61.pdf
Q5 b(ii) why we are taking 11C+11C3 instead of 8C5+8C3 wont it be the same then if the question asked for random selection
and can someone plz explain Q6 also
- Messages
- 1,824
- Reaction score
- 949
- Points
- 123
Please answer this questionFor a biased cubical dice the probability of any particular score between 1 and 6 (inclusive) being obtained is inversely proportional to that score. Find the probability of scoring a 1.
I don't know .. I think this is what it will be... What's the answer?
1 ----- 2 ----- 3 ---- 4 ---- 5 ---- 6
x/1 + x/2 + x/3+ x/4 + x/5 + x/6 = 1
49x/20 = 1
x = 20/49
Probability of 1 = x/1
= 20/49 Answer
what i thought at first thought but i dont know if it is riteI don't know .. I think this is what it will be... What's the answer?
1 ----- 2 ----- 3 ---- 4 ---- 5 ---- 6
x/1 + x/2 + x/3+ x/4 + x/5 + x/6 = 1
49x/20 = 1
x = 20/49
Probability of 1 = x/1
= 20/49 Answer
- Messages
- 382
- Reaction score
- 315
- Points
- 73
http://papers.xtremepapers.com/CIE/...S Level/Mathematics (9709)/9709_s10_qp_12.pdf
Please help me with qn no. 11 (ii & iii).
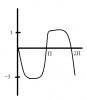
I've tried to sketch the graph (Attachment)... please check if its correct. For (iii), I'm totally confused!
Thanks
Please help me with qn no. 11 (ii & iii).
I've tried to sketch the graph (Attachment)... please check if its correct. For (iii), I'm totally confused!
Thanks
Attachments
ii seems correct as all it required was a graphhttp://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_s10_qp_12.pdf
Please help me with qn no. 11 (ii & iii).
I've tried to sketch the graph (Attachment)... please check if its correct. For (iii), I'm totally confused!
Thanks
iii basically it is asking for for those values of k for which the line y = k does not intersect each other so k>2 k<-3
- Messages
- 382
- Reaction score
- 315
- Points
- 73
For ii, the answer is k < 1, k > 7ii seems correct as all it required was a graph
iii basically it is asking for for those values of k for which the line y = k does not intersect each other so k>2 k<-3
- Messages
- 381
- Reaction score
- 140
- Points
- 53
plz help me, im terrible at mechanics.
- Messages
- 381
- Reaction score
- 140
- Points
- 53
http://papers.xtremepapers.com/CIE/...AS Level/Mathematics (9709)/9709_w08_qp_3.pdf
question no. 9 please please please help :/
and
http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_s09_qp_3.pdf
question number 6
The parametric equations of a curve are
x = a cos^3 t, y = a sin^3 t,
where a is a positive constant and 0 < t < pie/2
(i) Express dy/dx in terms of t. [3]
(ii) Show that the equation of the tangent to the curve at the point with parameter t is
x sin t + y cos t = a sin t cos t.
I've done part one. How do you do part (ii) ?
please help! Thanks in advance
question no. 9 please please please help :/
and
http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_s09_qp_3.pdf
question number 6
The parametric equations of a curve are
x = a cos^3 t, y = a sin^3 t,
where a is a positive constant and 0 < t < pie/2
(i) Express dy/dx in terms of t. [3]
(ii) Show that the equation of the tangent to the curve at the point with parameter t is
x sin t + y cos t = a sin t cos t.
I've done part one. How do you do part (ii) ?
please help! Thanks in advance