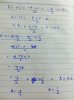can u upload the figure?Yes. Its OA + OB.
-
We need your support!
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Maths, Addmaths and Statistics: Post your doubts here!
- Thread starter OakMoon!
- Start date
- Messages
- 1,665
- Reaction score
- 2,400
- Points
- 273
as u know retartdation is -2This as well.
***amd***
let x be the unknown speed at 15
so -2=x-50/15-0
through the formula of the gradient or acceleration ...which ever u like..
no that is given in the question
Alright, I didn't know it was givenits simple maaaan!
3rt of 5 is givenm, and 3rt of 1000 is 10. do u need time even for this?
- Messages
- 2,738
- Reaction score
- 6,309
- Points
- 523
And the other question?as u know retartdation is -2
let x be the unknown speed at 15
so -2=x-50/15-0
through the formula of the gradient or acceleration ...which ever u like..
- Messages
- 510
- Reaction score
- 607
- Points
- 103
http://papers.xtremepapers.com/CIE/...(Calculator Version) (4024)/4024_w06_qp_1.pdf
Question 12 part c Samjha do koi. :/
Question 12 part c Samjha do koi. :/
- Messages
- 3,412
- Reaction score
- 9,812
- Points
- 523
And the other question?
Which ones?
- Messages
- 510
- Reaction score
- 607
- Points
- 103
http://papers.xtremepapers.com/CIE/...(Calculator Version) (4024)/4024_w06_qp_1.pdf
Question 22 aii as well.
Question 22 aii as well.
answer is 20?This as well.
***amd***
- Messages
- 2,738
- Reaction score
- 6,309
- Points
- 523
- Messages
- 2,738
- Reaction score
- 6,309
- Points
- 523
Woh speed time wala hai mje, leave it.answer is 20?
Tell the other one.
- Messages
- 3,412
- Reaction score
- 9,812
- Points
- 523
-9+3/2 = -3
f(t) = t+3/2
Add them both up, and simplify them, and then compare with A + Bt.. to get values of A and B..
- Messages
- 2,738
- Reaction score
- 6,309
- Points
- 523
-6+t+3/2= -3+t/2-9+3/2 = -3
f(t) = t+3/2
Add them both up, and simplify them, and then compare with A + Bt.. to get values of A and B..
-3+t/2= A+ Bt
Now how to compare them? :/
- Messages
- 3,412
- Reaction score
- 9,812
- Points
- 523
-6+t+3/2= -3+t/2
-3+t/2= A+ Bt
Now how to compare them? :/
You made an error.
See exploded dipers working, that is how you do it.
- Messages
- 2,738
- Reaction score
- 6,309
- Points
- 523
This is what he has written, I guess.You made an error.
See exploded dipers working, that is how you do it.
- Messages
- 2,738
- Reaction score
- 6,309
- Points
- 523
I got that. Thanks.Is this the correct answer?View attachment 43661I think its like this...
- Messages
- 1,229
- Reaction score
- 740
- Points
- 123
But why would it be equal to the straight line 's gradient?for the gradient draw the tangent . mark 2 point and find gradient. i cant to dat on screenproperly
- Messages
- 1,665
- Reaction score
- 2,400
- Points
- 273
kI got that. Thanks.
See it would be hard to find the gradient on a curve, won't it. So the line that we draw passes through the point on a curve. Since any point on a line will have the same gradient as the gradient of the line, the curve will also have the same gradientBut why would it be equal to the straight line 's gradient?