Physics: Post your doubts here!

[HumptyR]

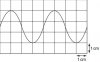
it's the diameter which has the largest effect. Look in the equation, d is a squared quantity. So the %age uncertainty in d would need to be doubled. So it will have the largest effect.

Thanks Thanks Thanks

 

[HumptyR]

The diagram shows a trace of a wave on a cathode-ray oscilloscope. The vertical and horizontal gridlines have a spacing of 1.0cm. The voltage scaling is 4Vcm–1 and the time scaling is 5ms cm–1.

What are the amplitude and period of the wave?

 

[HumptyR]

A steel sphere is dropped vertically onto a horizontal metal plate. The sphere hits the plate with a speed u, leaves it at a speed v, and rebounds vertically to half of its original height. Which expression gives the value of v/u?
A 1/2^2
B 1/2
C 1/√2
D 1-1/√2

 

[Rizwan Javed]

A steel sphere is dropped vertically onto a horizontal metal plate. The sphere hits the plate with a speed u, leaves it at a speed v, and rebounds vertically to half of its original height. Which expression gives the value of v/u?
A 1/2^2
B 1/2
C 1/√2
D 1-1/√2

It's C.

Take two situations here. First take the situation before the ball hits the metal plate. Let the distance it falls be 'h'.
Now you're given that the ball hits the metal plate with velocity 'u'. So apply an equation of motion here:

Vf^2 = Vi^2 + 2as

final velocity (Vf) is 'u', initial velocity (Vi) is 0 and distance fallen (s) is h. SO substitute these values into the equation, you'll get:

u^2 = 2ah <---- make 'h' the subject of this equation
h = u^2/2a -----equ (1)

Now consider the second situation when the ball rebounds after hitting. When ball rebounds, it leaves the plate with velocity 'v'. So this going to be our initial velocity in this situation. After rising a height of h/2 (as it said that it rises to half it's height of fall), it will come to rest momentarily. so it's final velocity at max height in this situation will be zero. Now again, substitute these values in to equation of motion mentioned above.

0^2 = v^2 -2a(h/2) <--- i have placed a minus sign before 2as, because the ball is decelarating here.

h = v^2/a ---- equ (2)

Now put the two equations: equ (1) and equ (2) equal, and solve.

You'll get v/u = 1/√2

 

[HumptyR]

It's C.

Take two situations here. First take the situation before the ball hits the metal plate. Let the distance it falls be 'h'.
Now you're given that the ball hits the metal plate with velocity 'u'. So apply an equation of motion here:

Vf^2 = Vi^2 + 2as

final velocity (Vf) is 'u', initial velocity (Vi) is 0 and distance fallen (s) is h. SO substitute these values into the equation, you'll get:

u^2 = 2ah <---- make 'h' the subject of this equation
h = u^2/2a -----equ (1)

Now consider the second situation when the ball rebounds after hitting. When ball rebounds, it leaves the plate with velocity 'v'. So this going to be our initial velocity in this situation. After rising a height of h/2 (as it said that it rises to half it's height of fall), it will come to rest momentarily. so it's final velocity at max height in this situation will be zero. Now again, substitute these values in to equation of motion mentioned above.

0^2 = v^2 -2a(h/2) <--- i have placed a minus sign before 2as, because the ball is decelarating here.

h = v^2/a ---- equ (2)

Now put the two equations: equ (1) and equ (2) equal, and solve.

You'll get v/u = 1/√2

You really are challenging the impossible

 

[HumptyR]

A ball is released from rest on a smooth slope XY.
It moves down the slope, along a smooth horizontal surface YZ and rebounds inelastically at Z. Then it moves back to Y and comes to rest momentarily somewhere on XY.


Which velocity-time graph represents the motion of the ball?

 

[Mr.Physics]

A ball is released from rest on a smooth slope XY.
It moves down the slope, along a smooth horizontal surface YZ and rebounds inelastically at Z. Then it moves back to Y and comes to rest momentarily somewhere on XY.

View attachment 58720
Which velocity-time graph represents the motion of the ball?
View attachment 58721

It's B I think

 

[HumptyR]

It's B I think

Nope the ans is A

 

[HumptyR]

It's B I think

At first I thought it was B too but the ans in ms is A, so I wanna know y the ans is A and y it is not B.

 

[Rizwan Javed]

Nope the ans is A

Yep it's A .

When the ball is released, the weight of the ball causes it accelerate uniformly. So it's speed increases uniformly (constant gradient). When it comes on to horizontal surface, it's speed becomes constant since now it's not accelerating anymore.

Then, it makes an inelastic collision with the wall, and loses it's K.E. Thus it's speed decreases as K.E=1/2mv ^2. So the velocity is smaller as compared to it's initial velocity. As the velocity is smaller now, so it'll take more time. This elimninates the option B.

Now when it again starts rising the slope, the weight plays it's role, decelrating the ball. As the acceleration of free fall remains same, so this gradient should be same as the gradient for the acceleration when the ball was falling down the slope.

Hope you'll understand.

 

[a_wiserME!!]

why wont the answer be C??

 

[HumptyR]

Yep it's A .

When the ball is released, the weight of the ball causes it accelerate uniformly. So it's speed increases uniformly (constant gradient). When it comes on to horizontal surface, it's speed becomes constant since now it's not accelerating anymore.

Then, it makes an inelastic collision with the wall, and loses it's K.E. Thus it's speed decreases as K.E=1/2mv ^2. So the velocity is smaller as compared to it's initial velocity. As the velocity is smaller now, so it'll take more time. This elimninates the option B.

Now when it again starts rising the slope, the weight plays it's role, decelrating the ball. As the acceleration of free fall remains same, so this gradient should be same as the gradient for the acceleration when the ball was falling down the slope.

Hope you'll understand.

Ofc I understood after all U explained it and thanks tho

 

[Mr.Physics]

Yep it's A .

When the ball is released, the weight of the ball causes it accelerate uniformly. So it's speed increases uniformly (constant gradient). When it comes on to horizontal surface, it's speed becomes constant since now it's not accelerating anymore.

Then, it makes an inelastic collision with the wall, and loses it's K.E. Thus it's speed decreases as K.E=1/2mv ^2. So the velocity is smaller as compared to it's initial velocity. As the velocity is smaller now, so it'll take more time. This elimninates the option B.

Now when it again starts rising the slope, the weight plays it's role, decelrating the ball. As the acceleration of free fall remains same, so this gradient should be same as the gradient for the acceleration when the ball was falling down the slope.

Hope you'll understand.

Cool
Thnx !!

 

[Rizwan Javed]

View attachment 58722

why wont the answer be C??

It's D.

The uncertainty in R can find by first finding the fractional uncertainties of I and V, and then adding them and multiplying by the the value of resistance calculated.

( 0.2/2 + 0.5/15 ) * 7.5

= -+1 ohm

 

[a_wiserME!!]

can someone tell me why the ans isnt B???! :'(

 

[HumptyR]

View attachment 58722

why wont the answer be C??

Ans is D, Because:
^R/R = ^I/I + ^V/V----- ^= Delta

R=V/I
R= 15/2=7.5

SO,
^R/R=^I/I+^V/V
^R=(^I/I+^V/V)R
^R=(0.2/2 + 0.5/15)*7.5 = 2

 

[a_wiserME!!]

Ans is D, Because:
^R/R = ^I/I + ^V/V----- ^= Delta

R=V/I
R= 15/2=7.5

SO,
^R/R=^I/I+^V/V
^R=(^I/I+^V/V)R
^R=(0.2/2 + 0.5/15)*7.5 = 2

It's D.

The uncertainty in R can find by first finding the fractional uncertainties of I and V, and then adding them and multiplying by the the value of resistance calculated.

( 0.2/2 + 0.5/15 ) * 7.5

= -+1 ohm

thank you!

 

[Rizwan Javed]

View attachment 58723
can someone tell me why the ans isnt B???! :'(

In this question we're told that the velocity is positive upwards. Also, we know that at highest & lowest points the mass will come momentarily to rest. So when mass is at lowest point, the velocity will be zero, and afterwards, when it'll again start moving upwards, it's velocity will be positive. this elimintes the chance of B being the answer as after coming to rest, the velocity is negative showing that the ball is moving downwards now.

Hope you understood.

 

[HumptyR]

In this question we're told that the velocity is positive upwards. Also, we know that at highest & lowest points the mass will come momentarily to rest. So when mass is at lowest point, the velocity will be zero, and afterwards, when it'll again start moving upwards, it's velocity will be positive. this elimintes the chance of B being the answer as after coming to rest, the velocity is negative showing that the ball is moving downwards now.

Hope you understood.

So is C the ans?

 

[Rizwan Javed]

So is C the ans?

No. As I explained above, it'll be mometarily at rest at lowest point, so it's velocity will be zero there. So it can't be C.

It's D.