- Messages
- 5
- Reaction score
- 0
- Points
- 11
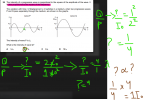
View attachment 64128 helpANS is B

W acts ats at centre of radius which is 0.20m. Now to lift Weight, you would need upward force. To provide that upward force, you would need torque o a couple as there are two forces acting in opposite directions but you only require one of them to act in direction opposing the Weight (ACWM).