- Messages
- 373
- Reaction score
- 1,091
- Points
- 153
Thank you.I think multiplying 20 times 3, would be wrong. Yes. you got the answer right, but the approach is wrong.
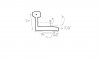
To calculate the resultant moment, we multiply the force and the perpendicular distance; in this case 2m for both 5N and 20N.
Now think about you how the 10N will have a resultant on the entire system as a whole. This is not just a simple bean and a pivot. One end of the system is bent at 90 degrees, and all the forces are acting on this end of the system. Now, for forces to have a resultant moment to this end, it has to act perpendicularly. And from the diagram we can see that the 10N is parallel not perpendicular. So the only two forces to have a resultant are the 5N and the 20N. The 10N is a trick, and is there to confuse you.
Now, f1d1-f2d2=0
20(2)-5(2)
40-10= 30 Nm. Hence, answer is A.
I've tried explain question 13 above.
Question 16-
The derivate of an energy/time graph will give us the power. We can see the graph is steepest from 10J to 40J. So the gradient=
(40-10)/(3-2)= 30W
Question 25-
I is directly proportional to A^2 (A square)
So 2I is proportional to x^2 (Since we need to find the corresponding amplitude, let's assume it to be x).
Now a ratio calculation-
2IA^2= Ix^2
2A^2=x^2 (I gets cancelled with each other)
so square root of 2A^2=x
The square root cancels indice of A ("the raised to the power 2"). which leaves us with "square root" of 2 * A.
I know it's complicated, but I hope you get it.
Question 33
We use the formula
R=("row"L)/A
L is directly proportional to R. and A is inversely proportional to R. It is mentioned in the question that the length is doubled. So since L is proportional to R, R will also be doubled. But they also mentioned that the volume remains constant. Now for a wire, whose length has been double, and for it's volume to remain constant, there has to be a reduction in the crossectional area of the wire; and in our case, since the length has been doubled, the coressectional area has to be halved, in order for the volume to remain constant. Now how will this increase in length, but the decrease in area, affect the resistance over all? The doubling of the length doubles the resistance, since it's directly proportional. And halving the area, will again double the resistance, since the area is inversly proportional. So in total, the resistance would be increased by a factor of 4. Hence the answer is D, 4R.
And as for question 14, I really can't do it, and need help myself.