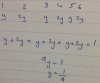Statistics S1 post your doubts here

[Talha Irfan]

http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_s13_qp_62.pdf
Question 4 all. Benn bothering me for sometime now

i) P of a number being less than or equal to four = 4/9
X - Bin(5,4/9)
P(X>=2) = 1 - [ P(X=0) + P(X=1)]
By solving this binomial expression, you will get the answer 0.735

ii) less than or equal to 4 had probability of 4/9
less than or equal to 3 will have probability of 3/9
so less than or equal to k will have a probability of k/9 . Agreed?

so again X - Bin(n, k/9)

Mean = np => n * k/9 = 96
Variance = npq => n * (k/9) * (1 - k/9) => n * (k/9) * ((9-k)/9) = 32

solve both the equations simultaneously preferably with the equation division method

 

[ZaqZainab]

The cards include 12 picture cards, 20 odd cards and 20 even cards. how many of the sequences will contain 3 picture cards, 3 odd numbered cards and 2 even numbered cards.
answer= 3.097*10^12

 

[Harsh Poddar]

I've made this site that can be used to quickly access past papers to all the subjects of IGCSE, and AS and A level students. Try it out and please give feedback. Already being used by 1100+ users across 53 countries.

IGCSE: gopapers.net/igcse.html
A & AS Level: gopapers.net/alevel.html

 

[Talha Irfan]

I've made this site that can be used to quickly access past papers to all the subjects of IGCSE, and AS and A level students. Try it out and please give feedback. Already being used by 1100+ users across 53 countries.

IGCSE: gopapers.net/igcse.html
A & AS Level: gopapers.net/alevel.html

Perfect Job! Well Done!

 

[Talha Irfan]

The cards include 12 picture cards, 20 odd cards and 20 even cards. how many of the sequences will contain 3 picture cards, 3 odd numbered cards and 2 even numbered cards.
answer= 3.097*10^12

Is this the complete question :
Eight cards are selected with replacement from a standard pack of 52 playing cards.?
The cards include 12 picture cards, 20 odd cards and 20 even cards. How many different sequences of eight cards are possible. Also, how many of the sequences will contain 3 picture cards, 3 odd numbered cards and 2 even numbered cards.

 

[ZaqZainab]

Is this the complete question :
Eight cards are selected with replacement from a standard pack of 52 playing cards.?
The cards include 12 picture cards, 20 odd cards and 20 even cards. How many different sequences of eight cards are possible. Also, how many of the sequences will contain 3 picture cards, 3 odd numbered cards and 2 even numbered cards.

yes

 

[Kamihus]

I've made this site that can be used to quickly access past papers to all the subjects of IGCSE, and AS and A level students. Try it out and please give feedback. Already being used by 1100+ users across 53 countries.

IGCSE: gopapers.net/igcse.html
A & AS Level: gopapers.net/alevel.html

Great job but maybe you should add O-Level too.

 

[Talha Irfan]

yes

Tricky one :
First, notice that the experiment is being conducted with replacement
So, in order to choose 8 cards from 52 cards, we perform combination
(12C1*12C1*12C1)x(20C1*20C1*20C1)x(20C1*20C1)
(for all three categories of cards, remember that we are not taking them at once we pick the card, keep it back, then again pick it up randomly therefore using nCr notation separately for each one)
once we have selected eight of them we have to arrange them so they are like PPPOOOEE arrangements will be 8! / 3!*3!*2!

==> (12C1*12C1*12C1)x(20C1*20C1*20C1)x(20C1*20C1) x 8! / 3!*3!*2! = 3.097*10^12 (Answer)

OR precisely (20)^3 x (20)^2 x (12)^3 x 8! / (3!*3!*2!)

 

[safa adil]

http://papers.xtremepapers.com/CIE/...S Level/Mathematics (9709)/9709_s13_ms_62.pdf
3 ii anyone ??

 

[Talha Irfan]

http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_s13_ms_62.pdf
3 ii anyone ??

you just posted the mark scheme

 

[Talha Irfan]

http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_s13_ms_62.pdf
3 ii anyone ??

There are equal deviations about the mean, so right side deviation equals left side deviation. We can half the probability to get probability from mean to right 445 + c and then add it to 0.5 for remaining left half of the curve
so now we get the condition :
P(X < 445 + c) = 0.94/2 + 0.5
P(X < 445 + c) = 0.97
P(z < (445 + c -445) / 3.6) = 0.97
solve for c
c = 6.77

 

[ZaqZainab]

http://papers.xtremepapers.com/CIE/...S Level/Mathematics (9709)/9709_w09_qp_62.pdf
Q1 part ii how exactly do you know the probability is 0.75? is it just an estimate

 

[_Ahmad]

http://papers.xtremepapers.com/CIE/Cambridge International A and AS Level/Mathematics (9709)/9709_w09_qp_62.pdf
Q1 part ii how exactly do you know the probability is 0.75? is it just an estimate

No
since this Box whisker plot is symmetrical (because the mean you got is in the middle of 39 and 63)
due to symmetry of the plot we can say that upper quartile is 75% of the data here the upper quartile is 63
so
P(X less than 63)=0.75

 

[Haya Ahmed]

First Query :

The scene is going on such that there are 4 holes shown and they're telling you different combination of identical and non-identical pegs to calculate number of ways they can be arranged.

i) 6 non identical pegs : four of them to be arranged within those holes = 6C4 (choose 4) * 4! (arrange four of them) = 360

ii) 2 Blue 1 Orange 1 Yellow so no choice has to be made as there are four pegs and four holes so BBYO ; arrange distinctly = 4!/2! = 12

iii) Now a pair of pegs are given of each colour, this part requires all distinct. So total 6 different coloured pegs that can be chosen = 6C4 * 4! = 360

iv) Three different means, for e.g. BBGO, OOGR ; which implies that there must be a pair of a single colour present , Let me call for pairs so from 6 pairs I need one
6C1 * (5C2 (5 different colours remaining and they both needs to be singly selected in order to achieve the required given condition and two are left as other two has already been selected of the same colour)) * 4!/2! (arrangement) = 720

v) Let us recount the possibilites

All different : DONE = 360
Three different : DONE = 720
Two different : Possible? Yes. BBYY so again from 6 pairs two pairs selection = 6C2 * 4!/(2!*2!) = 90
All same : Possible? eg YYYY : NO

Add all of them up : 1,170 ways

Hey Talha can you explain part iv and v again please ! .. what do you mean by 5C2 and why in (v) two different how did you get it !? .. thanks

 

[Kamihus]

Any list for the theory questions? Talha Irfan ZaqZainab

 

[Harsh Poddar]

Great job but maybe you should add O-Level too.

I'll be doing it soon enough. I'll try to add it by day after.

 

[ZaqZainab]

Any list for the theory questions? Talha Irfan ZaqZainab

nope

 

[ZaqZainab]

Haya Ahmed here Q5

 

[ZaqZainab]

Haya Ahmed Q7

 

[Princess Raven]

Can someone plz tell me why in part ii did they times 0.1587 by 2