PlanetMaster
XPRS Administrator
- Messages
- 1,177
- Reaction score
- 2,112
- Points
- 273
We are currently struggling to cover the operational costs of Xtremepapers, as a result we might have to shut this website down. Please donate if we have helped you and help make a difference in other students' lives!
Click here to Donate Now (View Announcement)
Hey redox233, I am not sure if you still need help on this, but let me explain this to you:-PlanetMaster can u pls explain this uestion? thankyou!


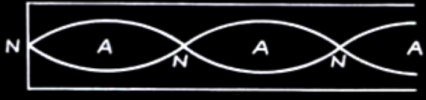
No worries pal. For both waves, we can take the points they intersect 0 displacement in the same direction.
Like this:View attachment 70545
A)a child of mass 35 kg movies down a sloping path on a skate board. the sloping path makes an angle 45 degree with the horizontal. the constant speed of the child along the path is 6.5 m/s. Calculate:
a) vertical dist through which child moves in 1.0s (done)
b) the rate at which potential energy is being lost (g=9.81 m/s^2) (confusion)
How is the answer to b) 80 J/s??
All I did was P = (35x9.81x0.51)/1 which gives answer 175 J/s (or 175 W)
Hey Hannah Moore.Hey everyone, if a person gets a wrong trend in the values in P3 physics Q.1. What is the procedure of marking for them.
I hope you are okay mate!Can I still fail if I pass? I must know, very important, what if I fail after I pass?? But I passed when I failed??!!? Tell me NOOOOOW, I am passing with fail on my exam tomorrow?
For almost 10 years, the site XtremePapers has been trying very hard to serve its users.
However, we are now struggling to cover its operational costs due to unforeseen circumstances. If we helped you in any way, kindly contribute and be the part of this effort. No act of kindness, no matter how small, is ever wasted.
Click here to Donate Now